Modelarea pietelor de optiuni

MODELAREA PIETELOR DE OPTIUNI

Pretul (prima) pe care cumparatorul unei optiuni il plateste si pe care vanzatorul acesteia il primeste este determinat, ca orice alt pret, de catre cererea si oferta pentru acea optiune. Cunoasterea modului de evaluare a optiunilor este importanta pentru dou 818j91i a motive: in scopul determinarii daca primele optiunilor existente sunt corecte si in scopul identificarii tranzactiilor profitabile si a oportunitatilor de arbitraj. Mai mult, modelele de evaluare a optiunilor sunt deseori folosite pentru evaluarea activelor ce nu sunt tranzactionate in cadrul burselor, dar care contin caracteristici ale unei optiuni. Practic, in prezent, majoritatea deciziilor manageriale sunt asimilate optiunilor, fiind evaluate cu ajutorul acestor modele.

Relatia de paritate put-call

O relatie importanta exista intre valoarea unei optiuni put si cea a unei optiuni call, care au aceeasi data de expirare, acelasi pret de exercitare si acelasi activ de baza (in cazul de fata, actiuni). In scopul demonstrarii acestei relatii si a concentrarii asupra relatiei de arbitraj, se presupune ca nu exista costuri ale tranzactiilor, marje sau taxe. Conform acestei relatii, pretul unei optiuni put europene, pe o singura actiune ce nu plateste dividende trebu-ie sa fie egal cu valoarea combinata a unei optiuni call, pe o actiune de acelasi tip, a unei pozitii short intr-o actiune de acelasi tip si a unei investitii virtual lipsite de risc (cumparare de obligatiuni guvernamentale), egala cu valoarea actualizata a pretului de exercitare.
Cu alte cuvinte, pretul de echilibru al optiunii este:

unde:

P = pretul curent al unei optiuni put europene asupra unei actiuni;

C = pretul curent al unei optiuni call europene asupra aceleiasi actiuni;

r = rata dobanzii aferenta unui credit fara risc, acordat pe durata de viata a optiunii;

t = timpul pana la expirarea optiunilor put si call;

K = pretul de exercitare a optiunilor put si call;

S = pretul curent al actiunii respective;

e^-rt = factorul exponential pentru calculul valorii actualizate.

Alternativ, pretul unei optiuni call europene trebuie sa fie egal cu pretul unei optiuni put, plus o suma egala cu pretul curent al activului de baza (pozitie long in activul respectiv), minus investitia fara risc a unei sume egala cu valoarea actualizata a pretului de exercitare.

Deci:

Daca oricare dintre aceste relatii nu este respectata, arbitragistii pot realiza un profit sigur, fara nici o investitie initiala, prin vanzarea optiunii supraevaluate si folosind suma obtinuta pentru cumpararea optiunii subevaluate si asumarea pozitiilor descrise mai sus in actiunile si obligatiunile respective.

De exemplu, daca preturile call sunt prea mari, in raport cu preturile put, arbitragistul poate realiza un profit sigur prin vanzarea unei optiuni call, concomitent cu cumpararea unei optiuni put, luarea cu imprumut a sumei egala cu K e^-rt la o rata de dobanda sigura si cumpararea activului de baza al optiunilor. Ultimele trei operatiuni creeaza
o pozitie sintetica long in optiunea call, care balanseaza pozitia short in aceeasi optiune.
In situatia inversa, daca preturile put sunt prea mari in raport cu preturile call, arbitragistul poate realiza un profit sigur prin vanzarea optiunii put supraevaluata, concomitent cu cumpararea optiunii call, acordarea unui imprumut egal cu K e^-rt la o rata de dobanda sigura si vanzarea activului de baza. In mod similar ultimele trei operatiuni creeaza o pozitie sintetica long in optiunea put, care balanseaza pozitia short in aceeasi optiune.

Factorii ce determina primele optiunilor

Pe parcursul duratei de viata a optiunii, deci inainte de data expirarii, valoarea sa depinde de urmatoarele variabile:

a.           pretul curent al activului de baza al optiunii;

b.          pretul de exercitare al optiunii;

c.          volatilitatea estimata a pretului activului de baza al optiunii;

d.          timpul ramas pana la expirarea optiunii;

e.          nivelul curent al ratei dobanzii pentru creditele lipsite de risc;

Acest set de variabile determina atat valoarea optiunilor call, cat si al celor put, dar nu in acelasi mod. In tabelul de mai jos este prezentat schematic impactul fiecaruia dintre acesti cinci factori asupra valorii optiunilor put si call, considerand celelalte patru variabile constante.

Impactul asupra optiunilor call

In determinarea valorii optiunii, importanta pretului activului de baza al optiunii si a pretului de exercitare al acesteia este evidenta. Mai putin evident, insa, este impactul volatilitatii pretului activului de baza. Volatilitatea poate fi interpretata ca masura a fluctua-tiei, deci a dispersarii preturilor posibile viitoare ale activului respectiv. Cu cat volatilitatea va fi mai mare, cu atat va creste si probabilitatea ca pretul activului sa atinga un nivel foarte ridicat sau foarte scazut: Detinatorul unei optiuni call are posibilitatea sa beneficieze din plin de o evolutie favorabila a pretului activului de baza, nefiind insa puternic afectat de o scadere a acestuia, deoarece in acest caz nu va exercita optiunea. In consecinta,
cu cat volatilitatea pretului va fi mai mare, cu atat si valoarea optiunii call va creste.
Timpul ramas pana la expirarea optiunii influenteaza valoarea sa, datorita relatiei existente intre acesta si volatilitate. Pe parcursul unei perioade mai indelungate, pot avea loc mai multe evenimente. Astfel, si un activ cu o volatilitate mai scazuta, poate, eventual inregistra o miscare favorabila a pretului. De aceea, primele optiunilor call sunt mai ridicate, cu cat timpul ramas pana la expirarea optiunii este mai mare.

Trebuie subliniat, insa, ca valoarea - timp a optiunii tinde catre zero odata cu apropierea datei de expirare, la scadenta devenind nula. Practica a dovedit ca valoarea - timp descreste intr-un ritm scazut in perioada de inceput a vietii optiunii, ritm ce se accelereaza pe masura ce data de expirare se apropie.

De asemenea, mai putin evident este si efectul ratelor dobanzii asupra valorii optiunii. Cu cat rata dobanzii este mai mare cu atat se va reduce valoarea actualizata a pretului de exercitare, pe care cumparatorul optiunii call s-a angajat sa-l plateasca in cazul exercitarii.

Astfel, o rata a dobanzii ridicata are acelasi efect precum un pret, de exercitare scazut, deci o crestere a valorii optiunii call. In plus, impactul ratei dobanzii trebuie evidentiat luand in considerare si timpul ramas pana la expirarea optiunii.
Valoarea actualizata a pretului de exercitare scade odata cu cresterea factorului timp; deci, acesta din urma, influenteaza valoarea optiunii si prin efectul sau asupra ratei dobanzii.
In cazul unei optiuni call, aceste efecte se consolideaza reciproc. Trebuie mentionat insa ca rolul ratei dobanzii in determinarea pretului optiunii este insa mult mai complex, variind insa in functie de activul de baza al optiunii. De exemplu, relatia direct proportionala dintre rata dobanzii si valoarea optiunii call pe actiuni nu este valabila si in cazul optiunilor pe contractele futures.

Impactul asupra optiunilor put

Efectele preturilor activelor de baza, ale preturilor de exercitare si ale ratelor dobanzii asupra valorii optiunilor put au un sens contrar fata de manifestarea lor asupra valorii optiunilor call. Ceilalti doi factori - volatilitatea activului de baza si timpul ramas pana la expirarea optiunii - actioneaza, insa, in acelasi sens, atat pentru optiunile call, cat si pentru cele put, marind probabilitatea evolutiei favorabile a pretului activului respectiv.

Calculul volatilitatii

Volatilitatea istorica

O modalitate de calcul a volatilitatii are la baza abaterea standard a schimbarilor procentuale anterioare ale pretului activului respectiv. Schimbarea procentuala a pretului se calculeaza deseori ca diferenta intre logaritmii naturali ai preturilor curente si cei ai preturilor anterioare. Ca urmare, abaterea standard a schimbarilor procentuale ale pretului se calculeaza dupa formula:

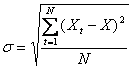
unde:

N = numarul observatiilor;

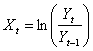respectiv al schimbarii procentuale a pretului;

Y_t = pretul activului in perioada t;

X = media aritmetica a lui X_t.

In functie de intervalul de date utilizat in calculul abaterii standard a preturilor, volatilitatea anuala se obtine prin inmultirea abaterii standard (calculata dupa formula de mai sus) cu radical din numarul perioadelor, respectiv:

pentru date lunare:

pentru date saptamanale:

pentru date zilnice:

In utilizarea acestei metode o atentie deosebita trebuie acordata selectarii perioadei de timp, care trebuie sa reflecte conditii similare cu cele existente pe perioada valabilitatii optiunii respective.

Volatilitatea dedusa

Aceasta metoda presupune estimarea volatilitatii prin deducerea ei cu ajutorul urmatorului model. Astfel, modelul se poate folosi pentru obtinerea volatilitatii, daca primele optiunilor existente pe piata se considera corect evaluate. Desi calculul ecuatiei in acest sens este dificil, rezultatul poate fi usor obtinut cu ajutorul software-ului de specialitate. Deseori, insa, primele optiunilor cu aceeasi data de expirare sunt diferite pentru acelasi activ. Ca urmare, apare problema alegerii volatilitatii deduse; in practica, aceasta este solutionata prin formarea unei medii ponderate a rezultatelor obtinute, medie ce poarta denumirea de atribuita optiunilor in bani si celor cu un volum mai mare de tranzactii, o piata mai activa fiind o piata mai eficienta.

Principii elementare legate de pretul optiunilor

Considerand:

C(t),P(t) = preturile curente ale optiunilor call/put americane pe o unitate spot de valuta de schimb;

c(t), p(t) = preturile curente ale optiunilor call/put europene pe o unitate spot de valuta de schimb;

C^*(t), P^*(t) = preturile curente interne ale optiunilor call/put americane pe contracte futures;
c^*(t), p^*(t) = preturile curente interne ale optiunilor call/put europene pe contracte futures;
C^**(t), P^**(t) = preturile curente interne ale optiunilor call/put americane de tip futures;
c^**(t), p^**(t) = preturile curente interne ale optiunilor call/put europene de tip futures;
K = pretul de exercitiu al optiunii;

S(t) rata de schimb spot curenta;

Z(t) = pretul curent al contractului futures;

B(t,T) = pretul curent al unei obligatiuni cu un discount simplu care are maturitatea la t + T si plateste o unitate de valuta interna la maturitate.

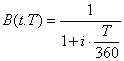
B^*(t,T) = pretul actualizat la momentul t al obligatiunii care plateste o unitate de valuta straina la maturitate.

Principiul 1

C(t), C^*(t), C^**(t) ³ P(t), P^*(t), P^**(t) ³

c(t), c^*(t), c^**(t) ³ p(t), p^*(t), p^**(t) ³

Principiul 2

La expirare:

C(t+T) = max [0, S(t + T) - K]

c(t+T) = max [0, S(t + T) - K]

C^*(t+T) = max [0, S(t + T) - K]

Principiul 3

La expirare:

P(t+T) = max [0, K - S(t + T)]

Principiul 4

Pentru t < T

C(t) ³ max [C(t), S(t) - K]

Principiul 5

Fiind date doua optiuni, ambele pe aceleasi sume ale aceleasi valute, cu acelasi pret de exercitiu dar cu termene de maturitate diferite, avem:

C(t + T) > C(t + T'), T' < T

c(t + T) £ c(t + T'), T' < T

restul variabilelor ramanand identice.

Principiul 6

Fiind date doua optiuni la care difera doar pretul de exercitiu, optiunea cu pretul de exercitiu mai mare va avea o valoare mai mica decat optiunea cu pretul de exercitiu mai mic.

Principiul 7

O optiune call pe o moneda straina poate fi considerata ca o optiune put pe moneda interna si invers, deoarece si rata de schimb poate fi ca rata de schimb intre moneda
straina si moneda interna si rata de schimb intre moneda interna si moneda straina.

Principiul 8

Fie o optiune europeana pe un contract futures care expira la aceeasi data cu contractul futures. Atunci:

Z(t + T) = S(t + T)

c(t) = c^*(t)

p(t) = p^*(t)

Observatie: ultimele doua relatii nu sunt aplicabile optiunilor americane.

Principiul 9

c(t) = B(t,T) c^**(t)

c(t) = B(t,T) c^**(t)

Aceste relatii sunt valabile pentru optiunile call si put europene.

Principiul 10

Consideram urmatoarele doua strategii de portofoliu, ce incep la acelasi moment de timp t, cand rata de schimb spot este S(t):

Strategia A:

cumpar la pretul c(S(t), K, t, T) o optiune call europeana cu un pret de exercitiu K care expira peste T zile, optiune pe o unitate de schimb spot;

cumpar K B(t,T) obligatiuni pe valuta interna. Suma totala de valuta interna investita: c + X B.

Strategia B:

cumpar o obligatiune pe valuta straina, cu maturitatea in T unitati de timp, la un pret curent in valuta interna: S(t) B^*(t,T). Suma totala de valuta interna investita: S B.

La momentul t +T:

rata de schimb spot este : S(t + T);

obligatiunile vor avea valorile: B(t+T,0) = 1

B^*(t+T,0)

- optiunea call va avea valoarea: c[S(t + T), K, T, 0] = max [0, S(t + T - K)]. Astfel:

Se observa ca strategia A costa mai mult decat strategia B. De aici rezulta ca:

cum C(t) ³ c(t) >

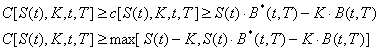
Similar pentru optiuni put europene si americane:

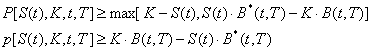
Principiul 11

Relatia de paritate:

, unde F = rata de schimb forward

inlocuind in relatia:

din principiul 10, obtinem:

Similar pentru optiunile put:

Principiul 12

Relatia de paritate put - call pentru optiuni europene pe spot:

Pretul unei optiuni put europene pe spot este total determinat de:

pretul unei optiuni call europene corespondente;

rata de schimb spot;

preturile obligatiunilor discount in cele doua valute.

Principiul 13

Utilizand relatia din principiul 11 si substituind-o in relatia din principiul 12, obtinem:

Pretul unei optiuni put europene difera de pretul unei optiuni call europene corespondente prin factorul ce reprezinta diferenta actualizata dintre pretul de exercitiu K si rata de schimb forward.

Modelul Black-Scholes

Modelul Black-Scholes este modelul de evaluare cel mai cunoscut si larg utilizat in managementul financiar modern. Creat initial in 1973 de catre doi teoreticieni, Fischer Black si Myron Scholes, acesta era destinat evaluarii optiunilor europene asupra actiunilor ce nu platesc dividende.

Fundamentul modelului il reprezinta crearea unui portofoliu ipotetic si lipsit de risc, format din pozitii call long si pozitii short in actiunile de baza ale optiunii, cu ajutorul caruia un investitor obtine ca profit rata dobanzii aferenta unui credit fara risc. Utilizand acest portofoliu impreuna cu operatii referitoare la preturile curente ale actiunilor si la ratele dobanzii si folosind ca ipoteza valorile probabile ale actiunilor in momentul expirarii optiunii, Black si Scholes au obtinut urmatoarea ecuatie pentru optiunile europene asupra actiunilor ce nu platesc dividende:

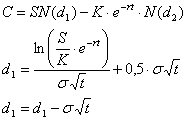
unde:

- C, S, K, r si t reprezinta aceleasi simboluri ca in formulele anterioare;

- s este volatilitatea anuala a actiunilor (calculata ca abatere standard);

ln(.) este logaritmul natural;

- N(.) este functia de distributie a probabilitatii cumulative pentru o variabila normal standardizata, intrucat modelul Black-Scholes presupune ca preturile actiunilor au o distributie log-normala, respectiv:

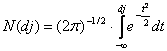
Dupa cum reiese de mai sus, utilizarea modelului Black-Scholes este relativ facila, pentru rezolvarea sa fiind necesare cinci variabile, dintre care patru sunt usor de obtinut: pretul curent al activului de baza al optiunii, pretul de exercitare, rata dobanzii si timpul ramas pana la expirarea optiunii. Cea de-a cincea variabila, insa, volatilitatea activului de baza al optiunii, nu este observabila in mod direct. Ca urmare, pentru obtinerea acesteia, in practica se utilizeaza doua metode.

Modelul binomial de evaluare a optiunilor

Modelul binomial de evaluare a optiunilor a fost dezvoltat de J. Cox, S. Ross si M. Rubinstein in 1979. Desi din punct de vedere cronologic, modelul binomial este succesor al modelului Black-Scholes, din punct de vedere matematic, el este, fara indoiala, predecesorul acestuia. Utilizat indeosebi la evaluarea optiunilor de tip american asupra actiunilor ce platesc dividende si a optiunilor tranzactionate OTC, acesta a devenit cea mai populara alternativa a modelului Black-Scholes.

Modelul binomial de evaluare a optiunilor pleaca de la ipoteza ca pretul activului de baza descrie un proces binomial multiplicativ, pe parcursul mai multor intervale de timp discrete. Astfel, se presupune ca valoarea activului de baza (S), in perioada imediat urmatoare va creste (u), sau va scadea (d), cu o anumita valoare. Astfel, in perioada imediat urmatoare, valoarea activului va fi, fie uS, fie dS, unde u > 1      si 0 < d < 1.

Modelul binomial cu un interval

Pentru demonstrarea modelului, s-a pornit de la urmatoarele ipoteze:

pretul curent al actiunii (S) fie va creste la uS cu o probabilitate q, fie va scadea la dS cu o probabilitate 1 - q;

optiunea call asupra acestor actiuni expira la sfarsitul perioadei urmatoare;

nu exista costuri ale tranzactiilor, taxe sau marje.

La expirare, valoarea optiunii va fi:

Cu = max (0, uS - K), daca pretul actiunii creste la uS sau

Cd=max(0, dS - K), daca pretul actiunii scade la dS, unde k este pretul de exercitare al optiunii.

Perioada 0                Perioada 1 Probabilitate

valoare valoare

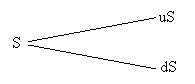q

1 - q

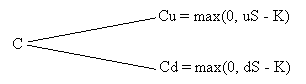
q

1 - q

Utilizand, de asemenea, un portofoliu ipotetic, avand aceeasi diagrama a profitului ca si o optiune call, la sfarsitul intervalului imediat urmator, deci, in cazul de fata la expirare, valoarea optiunii call este:

unde:

R = 1 plus rata dobanzii (r) aferenta creditelor fara risc, presupusa a fi constanta si pozitiva;

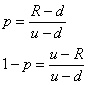
Cox si Rubinstein au demonstrat ca p este intotdeauna mai mare ca zero si mai mic decat unu, avand astfel proprietatile unei probabilitati.

Ecuatia de mai sus prezinta cateva caracteristici notabile. In primul rand, probabilitatea q nu apare in ecuatie; de aceea, evaluarea subiectiva a investitorului privind probabilitatea ca pretul actiunii sa creasca sau sa scada nu este necesara in evaluarea optiunii. in al doilea rand, formula nu depinde de atitudinea investitorilor fata de risc.
In al treilea rand, valoarea optiunii call depinde de o singura variabila necunoscuta, si anume, pretul actiunilor.

Modelul binomial cu mai multe intervale

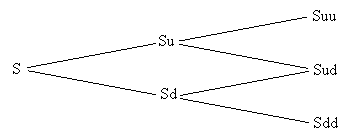
In practica, modelul cu un singur interval este nerealist; pretul unei actiuni se poate schimba de mai multe ori in timpul ramas pana la expirarea optiunii. Totusi, aceleasi principii de evaluare pot fi aplicate mai multor intervale de timp. Pentru obtinerea modelului cu mai multe intervale, formula de mai sus se extinde la doua intervale.
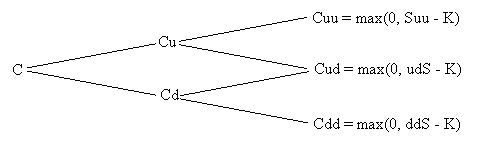
In acest caz, preturile posibile ale actiunilor si in functie de acestea preturile optiunii call respective sunt ilustrate in figura de mai jos:

Perioada Perioada 1 Perioada 2

valoare valoare valoare

sau

Valoarea optiunii call se obtine aplicand formula pentru cazul unui singur interval, pornind de la ultimul interval (2) catre momentul initial:

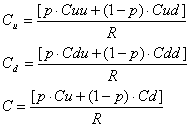
sau

Acelasi procedeu poate fi utilizat pentru obtinerea formulei generale cu n intervale de timp:

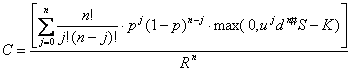
Modelul binomial de evaluare a optiunilor poate fi aplicat pentru diferite intervale de timp: luni, saptamani, zile sau chiar minute. In cazul unei optiuni cu un anumit timp ramas pana la expirare, pe masura ce intervalul se micsoreaza, numarul de intervale n creste. Astfel, formulele de evaluare bazate pe perioade de timp continue, de tipul modelului Black-Scholes nu reprezinta altceva decat formula de evaluare binomiala dedusa pentru un numar infinit de intervale de timp foarte mici.

Modelul Garman-Kohihagen

Modelul Garman-Kohlhagen este un model de evaluare a optiunilor valutare.
In anul 1983 Garman si Kohlhagen au modificat modelul Black - Scholes adaptandu-l la optiuni valutare. Pentru aceasta ei au tinut cont ca in cazul acestor optiuni apar doua rate ale dobanzii; acestea fiind ratele dobanzii unui credit fara risc ale celor doua valute care constituie activul de baza al optiunii.

Modelul Garman-Kohlhagen calculeaza prima optiunii call valutare ca fiind:

unde:

r_f = rata dobanzii pentru valuta straina (foreign currency) pana la data de expirare a optiunii;

r_d = rata dobanzii pentru valuta interna (domestic currency) pana la data de expirare a optiunii;

e^-rfS = reflecta faptul ca rata spot nu este pretul corect al activului, pretul corect fiind de fapt exprimat printr-o rata forward;

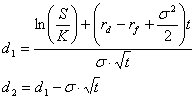
Asadar putem rescrie formula in modelul Garman-Kohlhagen in termeni forward:

unde:

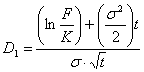
cu F = rata forward

Utilizand aceleasi notatii putem scrie formula pentru pretul optiunii put valutare, europene:

Acest model a fost adaptat de Garman si Kohlhagen pornind de la un model de baza si anume modelul Black - Scholes si este aplicabil optiunilor valutare europene.
Se face de asemenea ipoteza ca nu exista taxe de brokeraj si nici alte impozite.
In prezent modelele de evaluare a optiunilor se bucura de un succes considerabil, aplicarea lor extinzandu-se intr-un ritm rapid asupra majoritatii titlurilor financiare cu
caracteristici similare optiunilor. Ele sunt deosebit de utile in cadrul activitatii bursiere dar au ajuns sa depaseasca sfera acestei activitati, utilizate fiind din ce in ce mai mult pe plan international, in majoritatea deciziilor financiare.

Masurarea riscului optiunii si a senzitivitatii

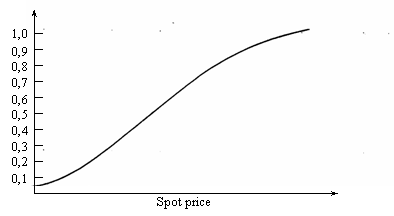Riscul unei optiuni e masurat de o serie de variabile la care dealerul, atunci cand are o lista cu preturile optiunilor, trebuie sa fie foarte atent. Variabile care masoara riscul sunt:
Delta unei optiuni refecta schimbarea in pretul optiunii care rezulta dintr-o schimbare de o unitate monetara in pretul activului de baza. Valoarea acestei marimi variaza intre 0 si 1 (sau 0% si 100%). Delta masoara variatia pretului optiunii la o modificare mica a ratei spot (pentru optiuni pe spot), sau a pretului futures (pentru optiuni pe futures). Graficul de mai jos ilustreaza cresterea valorii delta de la o valoare foarte joasa, cand optiunea este out-of-the-money la 1 cand optiunea este in-the-money. La acest moment optiunea este cu siguranta exercitata.

Am definit delta ca o schimbare in pretul optiunii atunci cand se schimba pretul activului de baza al optiunii. Aceasta inseamna ca delta poate fi definita ca panta tangentei la curba pretului optiunii. Ea masoara sensibilitatea pretului optiunii la modificarea pretului activului de baza. Mai mult, optiunea in-the-money este mai sensibila la modificarea pretului activului de baza. Pentru o optiune out-of-the-money o schimbare chiar mai mare in pretul activului de baza nu va avea efect. Un alt mod de a privi delta este sa spui ca ea masoara probabilitatea ca optiunea sa fie exercitata.

cand optiunea este out-of-the-money sunt sanse mici ca ea sa fie exercitata si delta este apropiata de zero;

cand optiunea este in-the-money probabilitatea sa fie exercitata este de 100% si delta va fi 1;

cand optiunea este at-the-money sansele sunt 50/50 si delta va fi 0,5.

Asadar delta poate fi utilizata ca o masura a riscului implicat de o pozitie pe option.

Gamma masoara sensibilitatea variabilei delta la modificarea pretului activului de baza, deci reprezinta suma cu care delta se schimba atunci cand pretul activului de baza se modifica foarte putin. Este deci o masura a stabilitatii variabilei delta.

O valoare gamma mare reprezinta o modificare rapida a valorii lui delta atunci cand pretul activului de baza se modifica. Uitandu-ne pe grafic vom observa ca:

delta nu se modifica mult atunci cand optiunea este out-of-the-money.
Asadar gamma, in acest caz are o valoare mica;

gamma are o valoare mica si atunci cand optiunea este in-the-money;

gamma este mare cand optiunea este at-the-money.

Gamma are de asemenea o valoare mare cand mai este putin pana la exercitarea optiunii si are o valoare mai mica cand timpul pana la expirarea optiunii e mai mare.

Un alt mod de a privi pe gamma este sa spunem ca ea arata daca curba este concava sau convexa si care este amplitudinea acestei convexitati sau concavitati. Asa cum delta masoara panta tangentei la curba la pretul curent, gamma masoara amplitudinea curbei la acest punct. Mai intuitiv se poate spune ca, daca delta este viteza schimbarii atunci gamma este acceleratia.

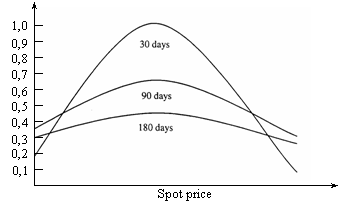
Figura de mai sus arata cum se modifica gamma pentru diferite nivele ale pretului activului de baza al optiunii si pentru diferite perioade de timp pana la maturitate.
Kappa (vega, zeta, epsilon, lambda) masoara impactul asupra primei optiunii atunci cand volatilitatea pretului activului de baza al optiunii se modifica cu un procent.
Daca o optiune este in-the-money sau out-of-the-money o schimbare in volatilitatea pretului activului de baza al optiunii nu inseamna prea mult, dar are un putemic efect atunci cand optiunea este at-the-money.

O mai mare volatilitate a pretului activului de baza al optiunii inseamna o valoare mai mare a primei optiunii, deoarece presupune o sansa mai mare ca optiunea sa fie exercitata in favoarea cumparatorului. Kappa afecteaza pretul optiunilor care au o perioada mai lunga pana la expirare.

In graficul de mai jos observam efectul lui kappa pentru diferite preturi ale activului si diferite zile pana la maturitate.

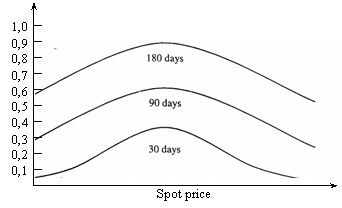
Theta masoara impactul timpului asupra pretului optiunii. Procentajul impactului este mai mare atunci cand mai sunt putine zile pana la expirarea optiunii. Impactul e mai mic cand mai sunt mai multe zile pana la expirarea optiunii. Theta are un mai mare impact asupra optiunilor at-the-money.

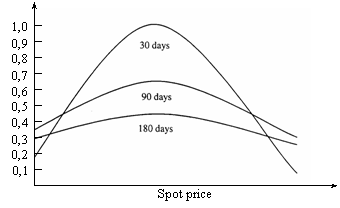Graficul de mai jos arata cum se modifica theta pentru diferite perioade de maturitate si diferite nivele ale pretului activului de baza al optiunii.

Rho masoara sensibilitatea pretului optiunii la rata dobanzii. Poate fi definit ca o schimbare in pretul optiunii la o modificare cu un procent a ratei dobanzii. Rho poate fi divizat in doua efecte:

primul e efectul schimbarii ratei dobanzii asupra pretului activului de baza care poate fi important daca optiunea este pe valuta ce se livreaza forward;

al doilea efect reflecta faptul ca o optiune este un instrument, o parghie.

Lambda (elasticitatea) arata cu cat se modifica (in procente) pretul optiunii pentru o modificare cu un procent a pretului activului de baza al optiunii.