
| ECONOMIE
Economia este o stiinta sociala ce studiaza productia si desfacerea, comertul si consumul de bunuri si servicii. Potrivit definitiei date de Lionel Robbins in 1932, economia este stiinta ce studiaza modul alocarii mijloacelor rare in scopuri alternative. Deoarece are ca obiect de studiu activitatea umana, economia este o stiinta sociala. |
| StiuCum
Home » ECONOMIE
» economie generala
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Modelul dinamic al firmei (van hilten) si extensii ale acestuia |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Modelul dinamic al firmei (van Hilten) si extensii ale acestuiaModelul dinamic al firmei (modelul van Hilten)Unul dintre cele mai importante modele dezvoltate in literatura de specialitate este acela in care firma este privita ca un sistem dinamic. Acest model analizeaza corelatia dinamica dintre investitiile facute din profiturile aduse de activele corporale, investitiile facute din credite si politica de dividende a firmei, in conditiile impozitului pe profit. Ipotezele modelului:Ipoteza 1. Firma are o productie omogena, iar functia de productie este liniara: Q(t) = q K(t) (1) unde: K(t) sunt bunurile de capital, exprimate valoric. Se face ipoteza ca o unitate de capital este egala cu o unitate monetara (s-a ales drept numerar unitatea de capital); - Q(t) reprezinta nivelul productiei, exprimat valoric; - q reprezinta productivitatea medie a
capitalului, Toata productia se presupune ca se vinde, astfel incat stocul de productie finita este zero.Ipoteza 2. Functia de vanzari S(Q(t)) este pozitiva, strict concava si satisface legea veniturilor descrescatoare la scala de fabricatie: S(Q(t)) = p(Q(t)) Q(t) (2) cu: - S(Q) - functia de venit; - p(Q(t)) - functia
inversa a cererii (piata produsului finit este cu competitie imperfecta);
Proprietatile functiei de vanzari arata faptul ca aceasta este crescatoare in raport cu productia si cu randamente descrescatoare la scala. De asemenea, productia nu poate fi negativa. Ipoteza 3. Singurul input este constituit de bunurile capital. Deprecierea capitalului (amortizarea) este proportionala cu valoarea capitalului aK(t), a fiind rata de amortizare. Venitul net din vanzari (profitul brut) este: K t = q p Q t - a K t (4) Ipoteza 4. Singurul tip de active corporale ale firmei, bunurile capital, pot fi finantate din imprumuturi si/sau actiuni: K(t) = X(t) + Y(t) (5) unde: X(t) - valoarea actiunilor; Y(t) - valoarea creditelor (imprumuturilor). Se cunosc, de asemenea, valorile initiale ale capitalului ( K(0) = K0), actiunilor (X(0) = X0) si imprumuturilor (Y(0) = Y0). Ipoteza 5. Cresterea valorii totale a actiunilor (a capitalului social) se realizeaza prin acumulari din profit.
unde: - - E(t) - partea din profit utilizat pentru cresterea valorii actiunilor. Profitul poate fi utilizat pentru investitii si/sau pentru cresterea valorii actiunilor. E(t) = (1 - f)·[Π(K(t)) - rY(t)] - D(t) (7) unde: - 636h71g f rata de impozitare a profitului corporal; - 636h71g r rata dobanzii; - 636h71g rY(t) valoarea dobanzii; - 636h71g (1 - f)[ (K(t)) - rY(t)] profitul net dupa impozitare si plata datoriilor. - 636h71g D(t) valoarea dividendelor; - 636h71g E(t) acumularile din profit sunt partea care ramane din profiturile corporale, dupa plata impozitului si a dividendelor. Ipoteza 6. Investitiile nete sunt:
unde: I(t) investitia bruta; aK(t) deprecierea capitalului.
Ipoteza 7. Volumul creditului este restrictionat la o pondere din valoarea capitalului social: Y(t) £ k X (t) (10) unde: k = ponderea maxima a imprumutului. Ipoteza 8. Costurile unitare depind de structura de finantare:
unde indicele N arata tipul de finantare: N = X finantarea din actiuni (autofinantare); N = Y finantarea din imprumut maxim; N = YX finantarea mixta. Ipoteza 9. Pentru demararea activitatii, venitul marginal in momentul initial depaseste costul marginal (oricare dintre costurile unitare):
S-a facut ipoteza ca costul unitar este egal cu costul marginal. Ipoteza 10. Firma se dezvolta numai daca venitul net din vanzari este pozitiv:
Ipoteza 11. Piata financiara si piata monetara se considera a fi doua piete distincte, astfel incat preturile pe cele doua piete sunt diferite:
unde: i este pretul pe piata financiara (considerat ca randament al actiunilor) - dividendele care revin la o unitate monetara platita de actionari pe actiuni; pentru firma i este un cost, este costul unei actiuni: firma trebuie sa asigure pentru fiecare unitate monetara platita de actionari pe actiuni, o revenire i. (1 - f)·r este costul unitar al creditului. intrucat rata de impozitare se aplica dupa plata datoriilor, la o unitate monetara profit net (dupa impozitare), revine mai putin de o unitate monetara dobanda. Este partea dintr-o unitate monetara de profit care revine pentru amortizarea creditului. Ipoteza 12. Valoarea actiunilor in momentul initial este strict pozitiva:
Performanta modelului: maximizarea valorii firmei calculata ca suma de dividende actualizate pe intervalul [0, T] si a valorii reale finale a capitalului social. Variabile de decizie (control): I(t) - investitia bruta; Y(t) - volumul creditelor; D(t) - valoarea dividendelor. Variabile de stare: X(t) - valoarea actiunilor; K(t) - valoarea bunurilor capital. Modelul dinamic al firmei
restrictii liniare asupra starii :
Observatie din ipoteza (7) rezulta ca
restrictii
liniare asupra comenzii D(t):
Þ restrictii
liniare asupra comenzii I(t):
Þ Aplicarea principiului lui PontreaghinConstruim Hamiltonianul problemei:
Lagrangeanul problemei:
Dinamica variabilelor adjuncte:
Conditiile (24) si (25) reprezinta conditii de maximizare a Lagrangeanului. Conditiile Kuhn - Tucker:
Eliminam cazurile in care I(t) si D(t) sunt pe limitele artificiale:
a) din
(24)
b) din
(25):
Calculam profitul marginal:
Transformam
ecuatiile de dinamica ale variabilelor adjuncte in ecuatie de dinamica a
multiplicatorului Inlocuim
in (34) pe
Conditiile de optim devin:
Analiza traiectoriilorExista 23 = 8 traiectorii posibile, dupa variatia (0;+) a celor trei multiplicatori m n n , din care trei sunt neadmisibile. Traiectorii neadmisibile1)
2) 3) cazul
Traiectorii de baza admisibileSe obtin din tabelul:
Traiectoria
nr. 1
(39)
Notam QYX* solutia ecuatiei S'Q = cYX. Pe traiectoria 1: S'Q este descrescatoare, deci Q(t) < QYX*; productia este mai mica decat valoarea stationara. Y(t)
= kX(t)
Pe traiectoria 1, actiunile cresc si imprumuturile cresc.
Din (38)
Traiectoria nr. 2
(39)
Inceputul traiectoriei 2:
Sfarsitul traiectoriei 2:
Traiectoria nr.3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Traiectoria |
Predecesor admisibil |
Cauza |
|
|
DA |
satisface 14 |
|
|
NU |
nu satisface 2 |
|
|
NU |
nu satisface 1 |
|
|
NU |
nu satisface 3 |
rezulta ca singura predecesoare posibila este traiectoria 1.
Predecesorii traiectoriei 1
|
Traiectoria 1 |
Predecesoare |
|
|
K(t) si Q(t) crescatoare |
Y(t) = k X(t) la sfarsitul predecesoarei Y(t) = k X(t)
Q(t) < ![]() pe traiectoria predecesoare Q(t) <
pe traiectoria predecesoare Q(t) < ![]()
i > (1 - f) r i > (1 - f) r
m (t) > 0 ![]() (t)
= 0
(t)
= 0
Nici una dintre traiectorii nu poate precede traiectoria 1.
Traiectoria de magistrala va cuprinde doar TR 5 sau succesiunea de traiectorii TR 1 TR 5, in functie de conditiile initiale:
|
Conditii initiale |
Traiectoria optima |
Evolutia capitalului |
|
X(0) = |
TR 5 |
K(t) = |
|
X(0) < |
TR 1 TR 5 |
K(t) = (1 + k) X(t) X(t) = |
Predecesorii traiectoriei
|
TR 4 |
La sfarsitul predecesoarei |
|
K(t) = X(t) Y(t) = 0 |
Y(t) = 0 |
|
Q(t) = |
Q(t) = |
|
i < (1 - f) r |
i < (1 - f) r |
|
m (t) = 0 |
|
TR 3 satisface simultan toate conditiile.
Predecesorii traiectoriei
|
TR 3 |
La sfarsitul predecesoarei |
|
Q(t) > |
Q(t) = |
|
i < (1 - f) r |
i < (1 - f) r |
|
Y(t) = 0 |
Y(t) = 0 |
Singura traiectorie care satisface aceste cerinte este traiectoria 2.
Predecesorii traiectoriei
|
TR 2 |
La sfarsitul predecesoarei |
|
|
Q(t) = |
Q(t) < |
|
|
|
|
i < (1 - f) r |
|
|
||
Singura traiectorie care satisface aceste cerinte este traiectoria 1.
Traiectoriile de magistrala, pentru cazul i < (1 - f) r, pot fi sintetizate, in functie de conditiile initiale, in tabelul de mai jos:
|
Conditiile initiale |
Traiectoria optimala |
|
X(0) = K(0) si X(0)
= |
TR 4 |
|
X(0) = K(0) si |
TR 3 TR 4 |
|
K(0) = |
TR 2 TR 3 TR 4 |
|
K(0) = (1 + k) X(0) si X(0)
< |
TR 1 TR 2 TR 3 TR 4 |
|
TR nr. |
Structura financiara |
Nivelul productiei |
|
|
D(t) |
Conditii de fezabilitate |
|
|
Y(t) = k X(t) |
Q(t) < |
|
|
|
|
|
|
0 < Y(t) < k X(t) |
Q(t) = |
|
|
|
|
|
|
Y(t) = 0 |
Q(t) > |
|
|
|
|
|
|
Y(t) = 0 |
Q(t) = |
|
|
|
i < (1 - f) r |
|
|
Y(t) = k X(t) |
Q(t) = |
|
|
|
i > (1 - f) r |
a) cY - costul finantarii din imprumut maxim
cY = ![]()
![]()
![]() cota parte din imprumut pe o unitate de
bun capital
cota parte din imprumut pe o unitate de
bun capital
Y(t) = k X(t), K(t) = (1 + k) X(t) ![]() =
= ![]() Y(t) =
Y(t) = ![]() K(t)
K(t)
r ![]() dobanda pe o unitate de bun
capital
dobanda pe o unitate de bun
capital
![]() rata de revenire a actionarilor, inainte
de plata impozitului. Dividendele se platesc dupa impozitare Þ inainte de impozitare trebuie
inclusa in cost valoarea
rata de revenire a actionarilor, inainte
de plata impozitului. Dividendele se platesc dupa impozitare Þ inainte de impozitare trebuie
inclusa in cost valoarea ![]() .
.
![]() partea dintr-o unitate monetara platita
pe actiuni, care revine la o unitate de bun capital. K(t) = (1 + k) X(t)
partea dintr-o unitate monetara platita
pe actiuni, care revine la o unitate de bun capital. K(t) = (1 + k) X(t) ![]() =
= ![]() Þ X(t) =
Þ X(t) = ![]() K(t)
K(t)
![]() costul unei actiuni (al dividendelor),
pe o unitate de bun capital.
costul unei actiuni (al dividendelor),
pe o unitate de bun capital.
a - costul deprecierii capitalului
![]() = costul total care revine la o unitate de bun
capital.
= costul total care revine la o unitate de bun
capital.
q = ![]()
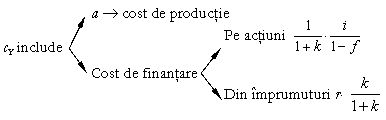
![]()
![]() = costul total pe o unitate de
produs finit.
= costul total pe o unitate de
produs finit.
Deci:
b) cYX = ![]() (a
+ r)
costul finantarii mixte (toate profiturile se reinvestesc si nu se platesc
dividende); finantare din imprumut maxim si actiuni.
(a
+ r)
costul finantarii mixte (toate profiturile se reinvestesc si nu se platesc
dividende); finantare din imprumut maxim si actiuni.
c) cX = ![]()
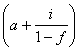 costul finantarii numai din
actiuni (imprumuturile sunt zero si se platesc dividende).
costul finantarii numai din
actiuni (imprumuturile sunt zero si se platesc dividende).
I) Cazul in care imprumuturile sunt ieftine (1 - f) r < i
Din analiza concatenaritatilor admisibile deducem:
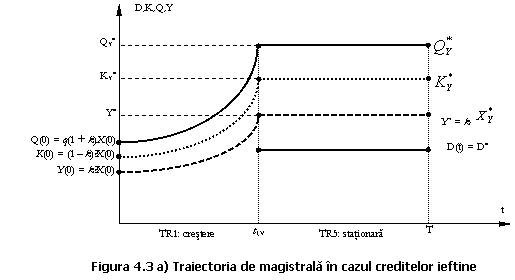
Q(0) = q (1 + k) X(0), deoarece K(t) = (1 - k) X(t).
Pe
traiectoria 1, K(t) < ![]() Þ X(0) <
Þ X(0) < ![]() .
.
Firma porneste de la valorile initiale si se
dezvolta intrucat ![]() >
0,
>
0, ![]() >
0,
>
0, ![]() >
0, cu credite maxime, pana in momentul in care
>
0, cu credite maxime, pana in momentul in care ![]() = cY,
moment in care firma comuta pe traiectoria stationara.
= cY,
moment in care firma comuta pe traiectoria stationara.
Pe traiectoria 1 venitul marginal din vanzari este mai mare decat costul marginal in cazul finantarii din imprumut maxim.
Dorim sa aratam ca aceasta conditie marginala implica faptul ca venitul marginal al unei actiuni este mai mare decat costul marginal al unei actiuni (dat de venitul minim i). Avem:
![]() profitul marginal al bunurilor capital;
profitul marginal al bunurilor capital;
![]() profitul marginal al bunurilor capital dupa plata datoriilor catre banca;
profitul marginal al bunurilor capital dupa plata datoriilor catre banca;
(1 - f ![]() profitul marginal al bunurilor
capital dupa plata datoriilor catre banca si dupa impozitare;
profitul marginal al bunurilor
capital dupa plata datoriilor catre banca si dupa impozitare;
k multiplicator al puterii de cumparare a capitalului social: deoarece K t k X t) rezulta ca o unitate monetara investita in capitalul social (pe actiuni) este egala cu (1 + k) unitati monetare de bunuri capital (datorita imprumutului) si mai departe, ca venitul marginal al unei actiuni (al unei unitati monetare investita in actiuni) este egal cu (1 + k venitul marginal al bunurilor capital (al unei unitati monetare investita in bunuri capital).
k f ![]() venitul marginal al unei
actiuni.
venitul marginal al unei
actiuni.
Pornind de la ![]() > cY
rezulta (1 + k f
> cY
rezulta (1 + k f ![]() > i, unde
i este costul marginal al actiunii.
> i, unde
i este costul marginal al actiunii.
Intr-adevar, din ![]() > cY si
tinand cont ca cY
> cY si
tinand cont ca cY ![]()
![]() rezulta q
rezulta q ![]() a >
a > ![]() si deoarece
si deoarece ![]() = q
= q ![]() a avem
succesiv:
a avem
succesiv: ![]() (1 + k) > k r +
(1 + k) > k r + ![]() Þ
Þ ![]() (1
+ k) - k r >
(1
+ k) - k r > ![]() Þ k f
Þ k f ![]() > i
> i
Daca venitul marginal al actiunii este mai mare decat
costul marginal al actiunii nu se platesc dividende (D t) =
0), actionarii reinvestind toate castigurile pana cand nivelul productiei Q t)
ajunge la nivelul ![]() corespunzator profitului maxim.
corespunzator profitului maxim.
Actionarii nu vor spori capitalul peste valoarea ![]() ,
deoarece va scadea atat venitul marginal al actiunii in raport cu costul sau
marginal, cat si venitul marginal din vanzari in raport cu costul marginal al
productiei. Rezulta ca
,
deoarece va scadea atat venitul marginal al actiunii in raport cu costul sau
marginal, cat si venitul marginal din vanzari in raport cu costul marginal al
productiei. Rezulta ca 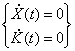 deci pe traiectoria 5 toate profiturile se
impart actionarilor:
deci pe traiectoria 5 toate profiturile se
impart actionarilor:
D t f p(![]() )
- r
)
- r ![]() f p(
f p(![]() )
- r k
)
- r k ![]()
II) Cazul in care actiunile sunt ieftine (la inceputul perioadei) i < (1 - f) r
In cazul traiectoriei de magistrala precedente, se pastreaza aceeasi structura de finantare pe intreg intervalul [0, T]: i > (1 - f) r
In cazul acestei traiectorii de magistrala se va schimba structura de finantare in timpul procesului de crestere.
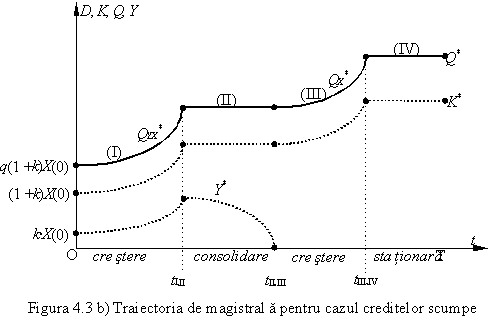
Cazul i < (1 - f) r la inceputul perioadei de crestere
TR . Firma isi demareaza activitatea cu o
valoare mica a capitalului social X(0) < ![]()
![]() .
In ciuda creditelor scumpe, firma porneste activitatea cu imprumut maxim,
datorita faptului ca venitul marginal din vanzari este mai mare decat costul
marginal al finantarii mixte (fiecare unitate de bun capital achizitionat din
imprumut va aduce un profit pozitiv) deci firma investeste la maxim din
imprumut si castig, rata de crestere a firmei fiind maxima.
.
In ciuda creditelor scumpe, firma porneste activitatea cu imprumut maxim,
datorita faptului ca venitul marginal din vanzari este mai mare decat costul
marginal al finantarii mixte (fiecare unitate de bun capital achizitionat din
imprumut va aduce un profit pozitiv) deci firma investeste la maxim din
imprumut si castig, rata de crestere a firmei fiind maxima.
Sa
aratam ca la inceputul traiectoriei 1, Q(t) < ![]() Þ
Þ ![]() > cYX Þ
profitul marginal al unei unitati de bun capital este mai mare decat costul de
finantare, daca finantarea s-ar face numai din imprumut (deci se justifica
imprumutul maxim).
> cYX Þ
profitul marginal al unei unitati de bun capital este mai mare decat costul de
finantare, daca finantarea s-ar face numai din imprumut (deci se justifica
imprumutul maxim).
![]() > cYX =
> cYX = ![]() a r
a r
![]() q
q ![]() - a
- a ![]() = (
= (![]() + a
+ a ![]() >
> ![]() a r
a r
![]() > r f
> r f ![]() > (1 - f r
> (1 - f r
Deoarece (1 - f ![]() > (1 - f r firma
va atrage imprumut maxim pentru a-si maximiza vanzarile.
> (1 - f r firma
va atrage imprumut maxim pentru a-si maximiza vanzarile.
Intrucat la inceputul perioadei de studiu actiunile sunt ieftine, firma va reinvesti toate castigurile (actionarii renunta la dividende).
Definim formula de parghie (legatura cu efectul de levier):
RE RT RT c ![]()
RE k f ![]() este
venitul marginal al actiunii
este
venitul marginal al actiunii
RT f ![]() este venitul marginal al capitalului dupa
impozitare
este venitul marginal al capitalului dupa
impozitare
c f r este costul marginal al imprumutului
Daca RT > c Þ ![]() (ponderea imprumutului) trebuie sa creasca pentru
ca venitul marginal al actiunii RE sa
creasca.
(ponderea imprumutului) trebuie sa creasca pentru
ca venitul marginal al actiunii RE sa
creasca.
Daca RT < c Þ ![]() trebuie sa scada pentru ca RE sa
creasca.
trebuie sa scada pentru ca RE sa
creasca.
In cazul traiectoriei 1 avem RT > c, deci
![]() trebuie sa creasca.
trebuie sa creasca.
TR : Cand
Q t) a devenit
egal cu ![]() Þ
Þ ![]() = cYX Þ
actionarii au trei posibilitati de impartire a castigurilor:
= cYX Þ
actionarii au trei posibilitati de impartire a castigurilor:
- 636h71g sa accepte plata dividendelor;
- 636h71g sa le utilizeze pentru dezvoltare (ajungandu-se la un venit marginal mai mic decat costul marginal al imprumutului (1 - f r, ceea ce este exclus;
- 636h71g sa utilizeze castigurile pentru plata datoriilor catre banci (pentru amortizarea creditelor, economisind (1 - f r pentru fiecare unitate de capital imprumutat.
Deoarece i < (1 - f) r, a treia varianta este cea mai economica Þ pana la momentul t2,3 firma isi achita toate datoriile, finalizand perioada de consolidare.
TR
: La sfarsitul traiectoriei 2,
dupa faza de consolidare, Q(t) < ![]() Þ S′(Q) > cX
=
Þ S′(Q) > cX
= ![]() a
a ![]() S′ =
S′ = ![]() [
[![]() + a] >
+ a] > ![]() a
a ![]() ) = cX
) = cX ![]() >
> ![]() (1 - f)
(1 - f) ![]() > i venitul marginal al bunurilor
capital este mai mare decat costul marginal al bunurilor capital finantate prin
actiuni Þ pe
traiectoria 3 investitia neta se face din actiuni (autofinantare).
> i venitul marginal al bunurilor
capital este mai mare decat costul marginal al bunurilor capital finantate prin
actiuni Þ pe
traiectoria 3 investitia neta se face din actiuni (autofinantare).
Dupa ce si-a platit datoriile firma incepe o
perioada de crestere pe traiectoria 3 prin autofinantare, pana cand Q(t) = ![]() ,
cand incepe traiectoria stationara, pe care se platesc dividende.
,
cand incepe traiectoria stationara, pe care se platesc dividende.
TR
: (1 - f) ![]() = i venitul marginal al capitalului
este egal cu costul marginal in cazul finantarii din actiuni Þ capitalul a
atins valoarea maxima Þ se
vor plati dividende:
= i venitul marginal al capitalului
este egal cu costul marginal in cazul finantarii din actiuni Þ capitalul a
atins valoarea maxima Þ se
vor plati dividende:
D t f p(![]() )
)
Conceptul de valoare prezenta neta (VPN) este utilizat in teoria economica pentru evaluarea proiectelor de investitii, compararea acestora si acceptarea sau respingerea lor.
Valoarea prezenta neta se defineste ca suma a valorilor prezente asteptate ale veniturilor lichide pe o perioada de timp, mai putin capitalul investit.
Daca VPN > 0, proiectul aduce o rata de revenire mai mare decat rata de scont. Rata de scont este egala cu costul de oportunitate al capitalului, respectiv venitul pe care il obtine firma investindu-si capitalul in proiecte alternative.
Consideram rata de scont egala cu rata de revenire asteptata a actionarilor.
Firma va accepta un proiect numai daca ![]() si va alege proiectul cu VPN maxima, adica:
si va alege proiectul cu VPN maxima, adica: ![]() .
.
Daca investitorul are un capital limitat, el va alege
proiectul care are indicele VPN maxim: ![]() .
.
Presupunem ca un investitor are W0 resurse monetare disponibile. Decizia intreprinzatorului va consta in partea din aceste resurse pe care le poate consuma in acest an si partea pe care trebuie sa o investeasca pentru a-si spori consumul in anul viitor.
Daca piata capitalului este perfect competitiva, pretul pe piata de capital este constant si egal cu rata dobanzii, de unde rezulta ca rata de revenire asteptata a individului este egala cu rata dobanzii.
Vom avea:
W0 = C0 + I0, unde:
W0 - capitalul investit initial;
C0 - consumul la momentul initial;
I0 - investitia la momentul initial.
Notam ![]() (randamentul investitiei)
(randamentul investitiei)
Daca ![]() ,
profitul perioadei 1, in ipoteza ca tot capitalul in momentul 0 a fost
investit.
,
profitul perioadei 1, in ipoteza ca tot capitalul in momentul 0 a fost
investit.
Functia de consum este f(C0, C1), cu:
![]() ;
f(C0, 0) = W0
;
f(C0, 0) = W0
curba de indiferenta a consumului intersecteaza coordonatele in punctele (W0, 0), respectiv (0, P
Curba de indiferenta a VPN este multimea combinatiilor (C0, C1) care aduc aceeasi VPN pentru W0 dat.
Punctul C* va fi punctul de tangenta al celor doua curbe de indiferenta.
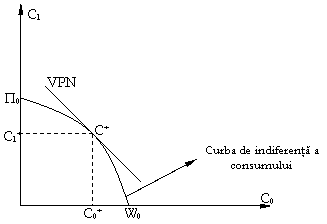
Notam cu i rata de
revenire asteptata a investitorului, egala cu rata de scont, egala cu costul de
oportunitate al capitalului.
(1) ![]()
![]() ,
, ![]() este valoarea prezenta a consumului in
perioada 1.
este valoarea prezenta a consumului in
perioada 1.
Ilustram in continuare mecanismul decizional de investitii pe MDF stuadiat anterior.
Definim investitia marginala ca sporul de venit adus de o unitate monetara suplimentara de investitie.
Traiectoria 4 m (t) = 0 n (t) > 0 n (t) = 0
![]()
![]()
![]()
![]() , dar m (t) = 0
, dar m (t) = 0![]()
Din ecuatia de evolutie a lui l (t) rezulta:
![]()
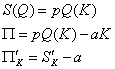
inlocuim n (t) in expresia lui ![]()
![]()
Integrand ecuatia diferentiala si tinand seama ca pe traiectoria 4 l (T) = 1, obtinem:
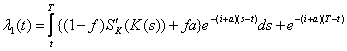
Dar l (t) = 1, rezultand ca pe traiectoria 4, VPN este:
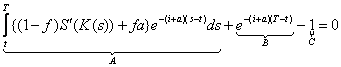
![]()
![]()
![]() este profitul marginal al unei unitati de capital.
este profitul marginal al unei unitati de capital.
![]() este profitul marginal dupa impozitare, adus
de o unitate de bun capital.
este profitul marginal dupa impozitare, adus
de o unitate de bun capital.
Observatii: In formula (2) termenii A, B, C au interpretarea:
A: - observam ca din profitul marginal dupa impozitare, lipseste termenul a, care este insa regasit in exponentiala.
- e-a(s-t) este partea dintr-o unitate de bun capital existent in momentul t care ramane (valoarea ramasa) in momentul s > t, tinand seama de contributia amortizarii.
- e-i(s-t) este valoarea actualizata a venitului produs in intervalul (s - t), s >t.
- termenul A reprezinta valoarea actualizata a profitului net (dupa taxare), pe intervalul [t, T].
B: - valoarea prezenta a unei unitati de bun capital (echipamente), existent in functiune la momentul T.
- e-a(T-t) este valoarea ramasa a capitalului in momentul T.
- e-i(T-t) este valoarea prezenta a unei unitati de capital social in momentul T.
C reprezinta cheltuielile de investitii de 1 u.m.
Membrul stang al relatiei (2) reprezinta venitul net actualizat al unei unitati monetare investite, deci VPN a investitiei marginale.
Din relatia (2) VPN a investitiei marginale este egala cu 0, de unde rezulta ca valoarea actualizata a fluxurilor de profit net egaleaza investitia marginala de o unitate monetara, deci firma a atins scala optima de fabricatie.
Expresia VPN pe traiectoriile 1, 2, 3 este data de multiplicatorul m (t), atasat restrictiei de nenegativitate a dividendelor.
m (t) reprezinta valoarea suplimentara a Lagrangeanului, daca limita minima a dividendelor descreste cu o unitate monetara. in acest caz, firma va dispune de o unitate monetara suplimentara pe care o va cheltui fie pentru investitii, fie pentru plata dividendelor.
VPN pe traiectoria 3:
(3)![]()
![]()
Pe traiectoria 3, m (t) > 0 Þ VPN a investitiei marginale este strict pozitiva, deci fluxul marginal de venituri este mai mare decat cheltuielile marginale de investitii, ceea ce inseamna ca pentru firma este optimal sa investeasca la maxim. Deoarece pe traiectoria 3, Y(t) = 0, finantarea cresterii pe traiectoria 3 se va face din actiuni.
Pe traiectoria 1, m (t) > 0 Þ VPN a investitiei marginale este strict pozitiva, deci este preferabil pentru firma sa investeasca la maxim. intrucat pe aceasta traiectorie Y(t) = kX(t), finantarea se va face din imprumut maxim si din actiuni.
Pe traiectoria 2, m (t) > 0, dar ![]() ;
este profitabil pentru firma sa-si amortizeze imprumutul, intrucat VPN scade.
Pe traiectoria 2, firma isi va opri cresterea si isi va amortiza imprumutul
(consolidare).
;
este profitabil pentru firma sa-si amortizeze imprumutul, intrucat VPN scade.
Pe traiectoria 2, firma isi va opri cresterea si isi va amortiza imprumutul
(consolidare).
Pe traiectoria 5 m (t) = 0 Þ VPN = 0 Þ firma si-a atins nivelul de echilibru, isi opreste dezvoltarea si plateste dividende.
Regula VPN este folosita pentru decizia de investitii a firmei, data fiind structura de finantare (cu ajutorul VPN nu se poate decide structura optima de finantare).
Costurile de ajustare sunt generate de cheltuielile de investitii ale firmei. Costurile de ajustare pot fi:
- costuri de ajustare interne: inlocuirea liniilor tehnologice si pregatirea fortei de munca generate de instalarea noului echipament;
- costuri de ajustare externe: practica marketingului de catre firmele furnizoare de capital, care poate duce la cresterea pretului activelor pe termen scurt.
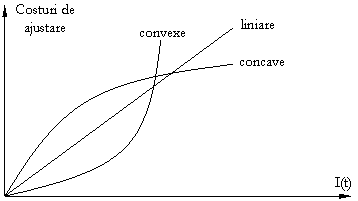
Se presupune ca A'(I) > 0, deci costurile de ajustare sunt crescatoare, si pozitive (A(I) > 0).
Se pune problema daca costurile marginale sunt constante,
crescatoare sau descrescatoare, in raport cu volumul investitiei:
A''(I) = 0 (costuri de ajustare liniare), A''(I) < 0 (costuri
de ajustare concave) sau A''(I) > 0 (costuri de ajustare convexe).
Situatia A''(I) > 0 (costuri de ajustare convexe) se aplica pietei monopsonice de capital (exista o singura firma care cumpara un anumit factor de productie).
in cazul in care A'(I) > 0 si A''(I) > 0, rata de crestere a costului va creste o data cu cresterea capitalului achizitionat; deci firma va controla cresterea capitalului.
Controlul cresterii capitalului (ajustarea) se va face in conformitate cu mecanismul acceleratorului flexibil.
![]()
unde I(t) = aK* = I* este investitia optima, K* este stocul dorit de capital (poate fi valoarea stationara a capitalului), iar a este coeficientul vitezei de ajustare (egal cu rata de amortizare).
Relatia (4) exprima faptul ca acumularea bunurilor capital este proportionala cu diferenta intre capitalul dorit si stocul de capital al firmei.
Transformam MDF in ipoteza ca nu exista posibilitatea de creditare.
Diferentele fata de MDF:
- nu exista credite;
- nu exista taxe pe profiturile corporale;
- exista costuri de ajustare.
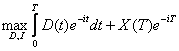
Relatia de balanta:
![]()
Functia costului de ajustare:
![]()
Functia de productie este liniara:
![]()
Functia vanzarilor este:
![]()
Ecuatia de crestere a valorii actiunilor este:
![]() ;
veniturile din vanzari, dupa scaderea deprecierii si a costurilor de ajustare
sunt folosite pentru autofinantare si plata dividendelor.
;
veniturile din vanzari, dupa scaderea deprecierii si a costurilor de ajustare
sunt folosite pentru autofinantare si plata dividendelor.
![]() ;
valoarea actiunilor in momentul initial este strict pozitiva.
;
valoarea actiunilor in momentul initial este strict pozitiva.
Ecuatia de evolutie a capitalului
![]()
![]()
![]()
![]()
Din relatia (6), ![]() ;
iar din (10) si (12):
;
iar din (10) si (12):
![]()
![]()
tinand seama de (16) si substituind X(t) prin K(t), obtinem:
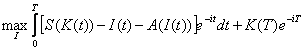
![]()
![]() (nenegativitatea dividendelor)
(nenegativitatea dividendelor)
![]()
![]()
Introducem o restrictie suplimentara care ne asigura ca
stocul de capital creste, atunci cand investitiile sunt mai mari decat
amortizarea capitalului (![]() ).
).
![]()
Functia Lagrangean
![]()
Conditiile de optim:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Solutia ![]() si
si ![]() este inadmisibila, intrucat ar rezulta D(t)
= I(t) . Raman 22
- 1 = 3 traiectorii admisibile.
este inadmisibila, intrucat ar rezulta D(t)
= I(t) . Raman 22
- 1 = 3 traiectorii admisibile.
|
Tr. |
|
|
I(t) |
D(t) |
Politica firmei |
|
|
|
|
max |
|
crestere maxima |
|
|
|
|
> 0 |
> 0 |
Politica de echilibru |
|
|
|
|
|
max |
restrangere |
Aplicandu-se procedura de cuplare, obtinem patru traiectorii optimale de magistrala:
TR I: tr 1 tr 2 tr 3
TR II: tr 2 tr 3
TR III: tr 3 tr 2 tr 3
TR IV: tr 3
Observam ca TR II si TR IV sunt incluse in TR I si TR III.
Se va alege una din traiectoriile de magistrala, in functie de VPN la inceputul perioadei.
· 636h71g VPN0 > 0, se alege magistrala I;
· 636h71g VPN0 = 0, se alege magistrala II;
· 636h71g VPN0 < 0, se alege magistrala III si IV.
Traiectoria de magistrala I, vpn0 > 0
Firma porneste activitatea pe traiectoria 1, nu plateste dividende, investeste toate castigurile, imprumuturile nefiind posibile.
Expresia VPN pe traiectoria 1 este:

Observatii
![]() este multiplicatorul lui Lagrange atasat
restrictiei de nenegativitate a dividendelor:
este multiplicatorul lui Lagrange atasat
restrictiei de nenegativitate a dividendelor: ![]() ;
dividendele sunt egale cu venitul net din vanzari si sunt pozitive; rezulta ca
investitiile si costul de ajustare trebuie sa fie maxim valoarea venitului din
vanzari S(K).
;
dividendele sunt egale cu venitul net din vanzari si sunt pozitive; rezulta ca
investitiile si costul de ajustare trebuie sa fie maxim valoarea venitului din
vanzari S(K).
![]() arata cresterea Lagrangeanului, daca se creste
cu o unitate monetara venitul net din vanzari (adica dividendele).
arata cresterea Lagrangeanului, daca se creste
cu o unitate monetara venitul net din vanzari (adica dividendele).
![]() exprima cheltuiala totala, pentru a se creste
cu o unitate monetara stocul de capital.
exprima cheltuiala totala, pentru a se creste
cu o unitate monetara stocul de capital.
![]()
![]() arata cresterea Lagrangeanului,
cand stocul de capital creste cu o unitate monetara.
arata cresterea Lagrangeanului,
cand stocul de capital creste cu o unitate monetara.
A: integrantul reprezinta fluxul prezent de lichiditati generat de valoarea ramasa a unei unitati monetare de bunuri capital achizitionata in momentul t si aflata in functiune in momentul s; integrala reprezinta valoarea prezenta a fluxului de lichiditati pe intervalul [t, T] generat de investitia de o unitate monetara in bunuri capital la momentul t, care se depreciaza in fiecare moment cu o rata a;
B: reprezinta fluxul de lichiditati indirect al investitiei.
Daca I(t) creste cu o unitate monetara, venitul va creste, iar limita
restrictiei ![]() va creste, in valori prezente, cu
va creste, in valori prezente, cu ![]() .
.
![]() arata cresterea valorii Lagrangeanului, daca
restrictia se relaxeaza cu o unitate monetara.
arata cresterea valorii Lagrangeanului, daca
restrictia se relaxeaza cu o unitate monetara.
![]() arata cresterea valorii Lagrangeanului cand
restrictia se relaxeaza (cu
arata cresterea valorii Lagrangeanului cand
restrictia se relaxeaza (cu ![]() ).
).
C: valoarea ramasa (in valori prezente) a unei unitati de bunuri capital, achizitionata pe intervalul [t, T], calculata in momentul T.
D: cheltuielile necesare la momentul t, pentru a creste stocul de capital cu o unitate monetara.
A+B+C+D: beneficiul net actualizat al unei investitii de o unitate monetara, pe intervalul [t, T] si deci VPN a investitiei marginale.
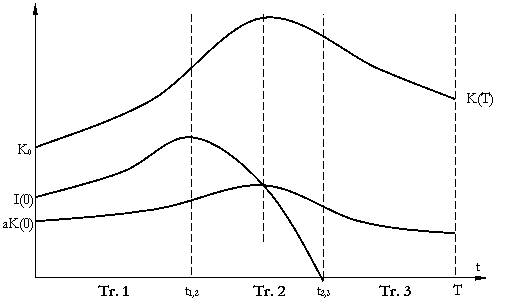
Pe Tr 1, ![]() creste,
intrucat
creste,
intrucat ![]() K(t)
creste si
K(t)
creste si ![]() descreste, pentru ca
descreste, pentru ca ![]() ;
va rezulta ca VPN va deveni la un moment dat zero si firma comuta pe Tr 2, unde
;
va rezulta ca VPN va deveni la un moment dat zero si firma comuta pe Tr 2, unde
![]() si va ramane zero pe toata perioada.
si va ramane zero pe toata perioada.
Relatia (31) devine:
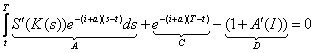
Deoarece ![]() investitiile
nu mai cresc, ele incep sa scada. Stocul de capital va creste in continuare,
pana cand
investitiile
nu mai cresc, ele incep sa scada. Stocul de capital va creste in continuare,
pana cand ![]() ,
dupa care incepe sa descreasca.
,
dupa care incepe sa descreasca.
Cand I(t) ajunge zero, traiectoria comuta pe Tr 3.
Expresia VPN pe Tr 3 este (pe Tr 3, ![]() expresia
lui VPN pe Tr 3 este data de
expresia
lui VPN pe Tr 3 este data de ![]() ):
):
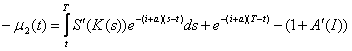
Din relatia (33) se vede ca VPN pe Tr 3 este negativa, deci firma nu va angaja in continuare investitii. Aceasta se datoreaza faptului ca din momentul t2,3, pana la sfarsitul perioadei T, timpul este prea scurt pentru a acoperi costurile de ajustare a noilor investitii; cheltuielile marginale depasesc fluxul marginal de lichiditati si este optimal pentru firma sa opreasca investitiile; in consecinta, valoarea capitalului in T va fi mai mica decat in t2,3.
Traiectoria de magistrala III, vpn0 < 0
Daca VPN0 < 0, firma demareaza activitatea pe Tr 3, pe care nu investeste nimic, in schimb va plati dividende.
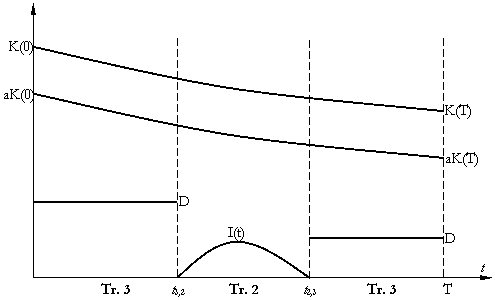
![]() ; stocul de capital va scadea si
venitul marginal (S'(K)) va creste.
; stocul de capital va scadea si
venitul marginal (S'(K)) va creste.
in momentul t3,2, S'(K)
a crescut suficient astfel incat ![]() este
indiferent daca I(t) > 0 sau I(t) = 0; deci I(t)
creste, dar pe perioada Tr 2 investitia nu atinge nivelul de inlocuire, astfel
incat K(t) continua sa scada pe Tr 2. intrucat
pe Tr 2, VPN = 0, I(t) incepe din nou sa scada, pana ajunge la
zero, cand se comuta pe
este
indiferent daca I(t) > 0 sau I(t) = 0; deci I(t)
creste, dar pe perioada Tr 2 investitia nu atinge nivelul de inlocuire, astfel
incat K(t) continua sa scada pe Tr 2. intrucat
pe Tr 2, VPN = 0, I(t) incepe din nou sa scada, pana ajunge la
zero, cand se comuta pe
Tr 3.
Scaderea investitiilor pe Tr 2 se datoreaza faptului ca firma are o capacitate de acumulare prea mica pentru a acoperi costurile mari de investitii, iar intervalul de timp pana la T este prea mic pentru a se recupera cheltuielile de investitii.
Pe Tr 3, VPN < 0, deci nu se investeste, se platesc dividende si capitalul scade.
Cazul in care T ¥ (T este foarte mare)
a) VPN0 > 0
Firma nu va mai comuta pe Tr 3.
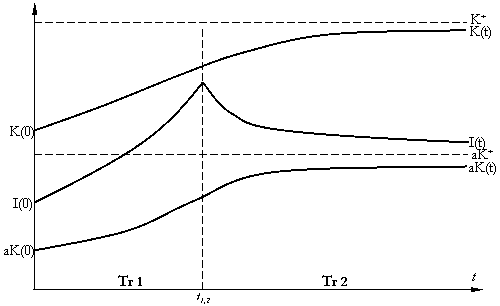
Pe Tr 2, investitiile tind
catre nivelul de depreciere, iar cresterea capitalului va fi data de mecanismul
acceleratorului flexibil:
![]()
Valoarea stationara K* este data de relatia:
![]()
Relatia de mai sus este derivata din conditia ca costul
marginal al unei unitati de bun capital pentru nivelul dorit K*
sa fie egal cu venitul marginal al unei unitati de bun capital pe intervalul
[t, ¥
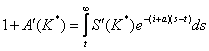
b) VPN0 < 0, T ¥
Traiectoria de magistrala nu mai comuta pe Tr 3; Tr 2 va fi cea finala.
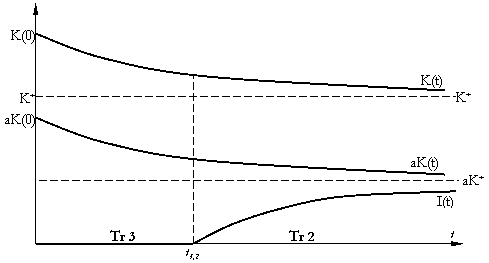
Pe Tr 2, sporul capitalului urmeaza mecanismul accelerator flexibil, iar nivelul stationar se atinge asimptotic.
VPN pe traiectoria 2:
Din conditiile de optim: ![]() ,
,
![]()
(25)![]() ,
ecuatie liniara de ordinul I, a carei solutie este:
,
ecuatie liniara de ordinul I, a carei solutie este:
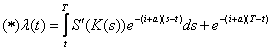
Pe traiectoria 2:
![]()
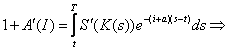
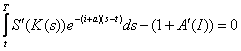
este expresia VPN pe traiectoria 2.
VPN pe traiectoria 1:
Din conditiile de optim: ![]() ,
,
![]()
![]()
Integram relatia de mai sus intre momentele de timp t si t1,2, intrucat in t1,2, firma comuta pe traiectoria 2:
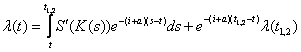
Calculam ![]() cu ajutorul relatiei
cu ajutorul relatiei ![]() si introducem in relatia de mai sus:
si introducem in relatia de mai sus:
![]()
![]()
Pe traiectoria 1: ![]() ,
,
![]()
inlocuim ![]() in expresia de mai sus:
in expresia de mai sus:
![]() +
+
![]()
care este relatia VPN pe traiectoria 1.
Concluzie Din aceasta succinta abordare a problematicii complexe a deciziei de investitii a firmei se deduce rolul foarte important al indicatorului VPN in angajarea de catre firma a fondurilor (proprii) de investitii, cand nu are posibilitatea de apelare la credite. Evident, demersul folosit in acest paragraf prin combinarea MDF cu teoria costurilor de ajustare si VPN se poate extinde si la alte modele, cercetare pe care o lasam pe seama cititorului care poate aduce astfel contributii personale in fundamentarea mecanismelor investitionale la nivel microeconomic.
Ipoteza 1: Firma produce un bun omogen folosind doi factori de productie: capitalul si munca.
Ipoteza 2: Modelul dinamic de analiza este un model cu factori de productie complementari, functia de productie este liniara, proportia intre factorii de productie ramanand constanta. Activitatea de productie este un proces prin care este fabricat produsul finit din munca si capital. Sunt presupuse doua activitati de productie:
activitatea 1: capital intensiva (raportul K/L este mare);
activitatea 2: forta de munca intensiva (raportul K/L este mic).
Functia de productie este data de:
(1) 636h71g 636h71g 636h71g Q(t) = q1K1(t) +q2K2(t)
unde Q(t) este productia fizica (omogena).
Veniturile sunt constante la scala de fabricatie (functia de productie este liniara).
Productivitatea medie a capitalului din activitatea j = 1,2 este:
qj = ![]() ,
j = 1,2
,
j = 1,2
Ecuatia de structura a fortei de munca este:
(2) 636h71g 636h71g 636h71g L(t) = l1K1(t) + l2K2(t)
iar compozitia organica a capitalului:
lj = ![]() ,
j =1,2
,
j =1,2
Ecuatia de formare a bunurilor capital:
(3) 636h71g 636h71g 636h71g K(t) = K1(t) + K2(t)
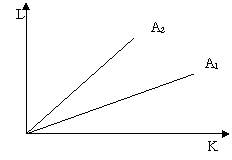
Ipoteza 3: Pentru activitatea 1 - activitate capital intensiva, vom avea conditiile:
K1 > K2
L1 < L2
de unde rezulta:
![]()
![]()
![]() productivitatea muncii este mai
mare in activitatea 1.
productivitatea muncii este mai
mare in activitatea 1.
Ipoteza 3':
Piata productiei finite este cu competitie imperfecta:
![]()
Ipoteza 4: Functia de castig:
(4) 636h71g 636h71g 636h71g S(K1(t), K2(t)) = (q1p(Q)-wl1) K1(t) + (q2p(Q)-wl2)K2(t)
Ipoteza 5: Singura sursa de finantare este autofinantarea:
X(t) = K(t)
Ipoteza 6: Ecuatia de evolutie a actiunilor:
![]() =
S(K1(t), K2(t)) - aK(t) - D(t); X(0) = K0 >
0
=
S(K1(t), K2(t)) - aK(t) - D(t); X(0) = K0 >
0
Ipoteza 7: Ecuatia de evolutie a bunurilor capital (investitia neta):
![]() =
I(t) - aK(t); K(0) = K0 > 0
=
I(t) - aK(t); K(0) = K0 > 0
Ipoteza 8: Functionala obiectiv:
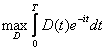 + X(T)e-iT
+ X(T)e-iT
Restrictii momentane:
(8) D(t)
![]() 0
0
(9) K1(t)![]() 0
0
(10) 636h71g 636h71g
K2(t)![]() 0
0
Din ![]() I(t)
- aK(t) = S(K1, K2) - aK(t) - D(t)
I(t)
- aK(t) = S(K1, K2) - aK(t) - D(t)![]()
D(t) = S(K1, K2)
- I(t)![]() 0
0
inlocuim X(t) cu K(t) si K2(t) cu K(t) - K1(t) si vom obtine modelul:
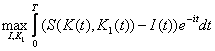 + K(T)e-iT
+ K(T)e-iT
![]() =
I(t) - aK(t); K(0) = K0 > 0
=
I(t) - aK(t); K(0) = K0 > 0
K(t) - K1(t)![]() 0
0
K1(t)![]() 0
0
S(K1(t), K2(t)) -
I(t)![]() 0
0
Rezolvarea modelului
Lagrangeanul problemei:
L(K(t),I(t),K1(t),l(t),m (t),m (t),m (t)) = (S(K(t), K1(t)) - I(t))(1+m (t)) + l(t)(I(t) - aK(t)) + m (t)(K(t) - K1(t)) + m (t)K1(t)
Conditiile de optim:
![]()
(19) ![]()
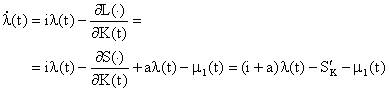
(21) 636h71g 636h71g m (t)(K(t) - K1(t)) = 0
(22) 636h71g 636h71g m (t)K1(t) = 0
(23) 636h71g 636h71g m (t) (S(K(t), K1(t)) - I(t)) = 0
(24) 636h71g 636h71g
m (t), m (t), m (t)![]() 0
0
(25) 636h71g 636h71g l(T) = 1
Datorita concavitatii Lagrangeanului si a restrictiilor, conditiile necesare sunt si suficiente.
Calcule preliminare
(26) 636h71g 636h71g Q(t) = (q1 - q2)K1(t) + q2K(t); L(t) = (l1 - l2)K1 + l2K(t)
S(K(t), K1(t)) = V(Q) - (wl1 - wl2)K1(t) - wl2K(t); V(Q) = p(Q)Q
(28) 636h71g 636h71g
![]() ;
; ![]()
(29) 636h71g 636h71g
![]()
(30) 636h71g 636h71g
![]()
Observatie
![]() ;
; ![]()
Costurile unitare:
(31) 636h71g 636h71g
cj
= 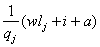 ,
c1
,
c1 ![]() c2
c2
![]() c21
c21
unde:
wlj - salariile pe o unitate de bun capital
i - revenirea pe o unitate de capital investit (de bun capital)
a - amortizarea pe o unitate de bun capital
(32) 636h71g 636h71g
c21 = ![]()
c21 - costul unitar al trecerii de la activitatea 2 la activitatea 1
Traiectorii posibile - sunt 23 = 8,
conform variatiei celor 3 multiplicatori mj(t), j = ![]() ,
din care 5 sunt traiectorii admisibile si 3 neadmisibile.
,
din care 5 sunt traiectorii admisibile si 3 neadmisibile.
|
Tr.. |
m (t) |
m (t) |
m (t) |
Activitatea |
|
Q |
Politica firmei |
|
|
|
|
|
|
|
<Q*21 |
crestere cu activitatea 2 |
|
|
|
|
|
|
|
Q*2 |
stationara, dividende, activitatea 2 |
|
|
|
|
|
|
|
Q*21 |
trecere de la activitatea 2 la activitatea 1 |
|
|
|
|
|
|
|
>Q*21 |
crestere cu activitatea 1 |
|
|
|
|
|
|
|
Q*1 |
stationara, dividende, activitatea 1 |
6) 636h71g m (t) > 0, m (t) > 0 Þ K(t) = K1(t), K(t) = 0 Þ K1(t) = 0 exclus prin ipoteza.
7) 636h71g m (t) = 0, m (t) = 0, m (t) = 0
din (19) Þ S'K = 0 Þ 0 = V'Q(q1
- q2) + w(l2 - l1)
Þ ![]() . Pe de alta parte (18) Þ l(t) = m (t) + 1 Þ
. Pe de alta parte (18) Þ l(t) = m (t) + 1 Þ ![]() ;
;
Cum m (t) = m (t) = 0 Þ din (20) Þ 0 = (i + a)(1+ m (t)) - S'K + m (t) Þ S'K = i +
a Þ q2V'Q =
S'K + wl2 Þ V'Q = (i + a
+ wl2)![]() =
c2, Þ
=
c2, Þ
Contradictie: venitul marginal din vanzari este simultan egal cu costul marginal al activitatii 21 si al activitatii 2.
Ipoteza:
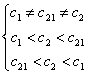 sau
sau ![]() ,
j = 1, 2, 21
,
j = 1, 2, 21
m (t) > 0, m (t) , m (t) > 0 - se regaseste aceeasi contradictie ca pentru traiectoria 6.
Traiectoria m m > 0, m > 0
Þ l(t) = 1 + m (t) Þ ![]()
Þ ![]() =
(i + a) (1+ m (t)) - S'K
=
(i + a) (1+ m (t)) - S'K
Þ K(t) > K1(t)
Þ K1(t) = 0; deci K(t) = K1(t) > 0
Þ S(K(t), K1(t)) - I(t) = 0 Þ D(t) = 0; deci nu se platesc dividende, tot ceea ce se castiga se reinvesteste.
S(K1(t),K2(t))
= I(t) Þ
![]() Þ
Þ ![]() (ecuatia de balanta fiind K(t) = X(t))
(ecuatia de balanta fiind K(t) = X(t))
Þ ![]()
Þ![]() Þ
Þ![]()
![]()
Pe traiectoria 1, ![]() .
.
la
inceputul traiectoriei: ![]()
la
sfarsitul traiectoriei: ![]()
La sfarsitul traiectoriei 1: ![]()
Traiectoria m (t) = 0, m (t) > 0, m (t) = 0
Þ l(t) = 1
Þ ![]()
Þ![]()
![]()
Þ 0 = (i + a) - S'K Þ S'K = (i + a)
Þ![]() , traiectoria 2 este stationara.
, traiectoria 2 este stationara.
Þ ![]() , se platesc dividende.
, se platesc dividende.
Þ K(t) = 0 Þ K(t) = K2(t)
Þ K(t) > K1(t) > 0; rezulta Q*2 < Q*21 Þ c21 < c2 < c1
Traiectoria m (t) = 0, m (t) = 0, m (t) > 0
Þ l(t) = m (t) + 1
Þ ![]() Þ
Þ ![]()
Þ ![]()
Þ K(t) = K1(t) Þ K2(t) = 0
Þ K1(t) > 0; deci rezulta ca ![]() si
si ![]() (este activitate de relocare)
(este activitate de relocare)
Þ ![]()
Pe traiectoria 3: m (t) > 0
- 636h71g 636h71g
la
inceputul traiectoriei: ![]() ,
,
![]()
![]() Þ (i + a)(1 + m (t)) - S'K >
0 Þ S'K < (i + a)(1 + m (t)) Þ (deoarece m (t) = 0) Þ S'K < (i + a) Þ
Þ (i + a)(1 + m (t)) - S'K >
0 Þ S'K < (i + a)(1 + m (t)) Þ (deoarece m (t) = 0) Þ S'K < (i + a) Þ ![]() Þ Q(t) > Q*2
Þ Q*21
> Q*2 Þ c1 < c2
< c21
Þ Q(t) > Q*2
Þ Q*21
> Q*2 Þ c1 < c2
< c21
Traiectoria m (t) > 0, m (t) = 0, m (t) > 0
Þ l(t) = m (t) + 1
Þ![]() Þ
Þ![]()
Þ ![]()
Þ K(t) = K1(t) Þ K2(t) = 0
Q(t) = (q1-q2)K1(t) + q2K(t) = (q1 - q2) K1(t) + q2K1(t) = q1K1(t)
![]() = V - (wl1 - wl2)K1(t)
- wl2K(t) = V - (wl1 -
wl2)K1(t) - wl2K1(t)
= V - wl1K1(t)
= V - (wl1 - wl2)K1(t)
- wl2K(t) = V - (wl1 -
wl2)K1(t) - wl2K1(t)
= V - wl1K1(t)
![]()
Pe traiectoria 4: m (t) > 0
la inceputul traiectoriei: ![]() ,
,
![]()
![]() Þ - S'K > m (t) - (i + a)(1 + m (t)) Þ S'K < - m (t) + (i + a)(1 + m (t)) Þ (deoarece m (t) > 0 Þ S'K < (i + a)(1 + m (t)) Þ S'K < (i + a) Þ
Þ - S'K > m (t) - (i + a)(1 + m (t)) Þ S'K < - m (t) + (i + a)(1 + m (t)) Þ (deoarece m (t) > 0 Þ S'K < (i + a)(1 + m (t)) Þ S'K < (i + a) Þ ![]() Þ Q(t) > Q*1
Þ Q(t) > Q*1
- la
sfarsitul traiectoriei 4: ![]() ,
,
![]()
![]() Þ S'K > i + a Þ
Þ S'K > i + a Þ ![]() Þ Q(t) < Q1*
Þ Q(t) < Q1*
Q < Q(t) < Q1* Þ c1 < c2 < c21
Traiectoria m (t) > 0, m (t) = 0, m (t) = 0
Þ l(t) = 1 Þ ![]()
Þ![]() Þ Q(t) > Q21*
Þ Q(t) > Q21*
Þ ![]() Þ - S'K = m (t) - (i + a) Þ S'K = i + a - m (t) Þ
Þ - S'K = m (t) - (i + a) Þ S'K = i + a - m (t) Þ ![]()
Þ K(t) = K1(t) Þ K2(t) = 0
Þ K1(t) > 0
Þ S(t) - I(t) > 0 Þ S(t) > I(t) Þ D(t) > 0
Observatie
![]() , deoarece
, deoarece ![]()
![]()
![]()
![]() Þ Q(t) = Q1*, traiectorie stationara.
Þ Q(t) = Q1*, traiectorie stationara.
Rezulta Q1* > Q21* Þ c1 < c2 < c21
Trebuie sa verifice conditiile de transversalitate:
l(T) = 1
l(T) = m (T) + 1 Þ m (T) = 0 Þ numai traiectoriile 2 si 5 pot fi traiectorii finale.
Traiectoria 2 este finala daca K(T) = K2(T) si c21 < c2 < c1.
Traiectoria 5 este finala daca K(T) = K1(T) si c1 < c2 < c21.
|
Tr. Nr. |
m (t) |
m (t) |
m (t) |
Activitatea |
|
Qt |
Politica firmei |
|
|
|
|
|
|
|
<Q*21 |
crestere cu activitatea 2 |
|
|
|
|
|
|
|
Q*2 |
stationara, dividende, activitatea 2 |
|
|
|
|
|
|
|
Q*21 |
relocare de la activitatea 2 la activitatea 1 |
|
|
|
|
|
|
|
>Q*21 |
crestere cu activitatea 1 |
|
|
|
|
|
|
|
Q*1 |
stationara, dividende, activitatea 1 |
TR1: Q(t) < Q2*; TR2: Q2*; K(t) poate fi continua si poate creste.
TR2: Q(t) = Q2*; TR2: Q(t) = Q21*; K(t) este discontinua, TR3 nu poate fi predecesoare.
TR2: c21 < c2 < c1; TR4: c1 < c2 < c21; contradictie.
TR5: K(t) = K1*; TR2: K(t)=K2*; discontinuitatea lui K(t).
|
Traiectoria 2 |
NU |
K discontinua |
|
Traiectoria 3 |
NU |
K discontinua |
|
Traiectoria 4 |
NU |
K discontinua |
|
Traiectoria 5 |
NU |
TR1: c21 < c2 < c1; TR5: c1 < c2 < c21 |
Traiectoria 1 |
NU |
K discontinua |
Traiectoria 2 |
NU |
inadvertenta de costuri |
Traiectoria 3 |
NU |
K discontinua |
Traiectoria 4 |
DA |
|
Traiectoria 1 |
NU |
K discontinua |
Traiectoria 2 |
NU |
inadvertenta de costuri |
Traiectoria 3 |
DA |
|
Traiectoria 4 |
NU |
K discontinua |
Traiectoria 1 |
DA |
|
Traiectoria 2 |
NU |
inadvertenta de costuri |
Traiectoria 3 |
NU |
K discontinua |
Traiectoria 4 |
NU |
K discontinua |
Traiectoria 1 |
NU |
K discontinua inadvertenta de costuri |
Traiectoria 2 |
NU |
K discontinua |
Traiectoria 3 |
NU |
K discontinua |
Traiectoria 4 |
NU |
K discontinua |
Concluzii a) Daca c21 < c2 < c1 Þ magistrala TR1 TR2
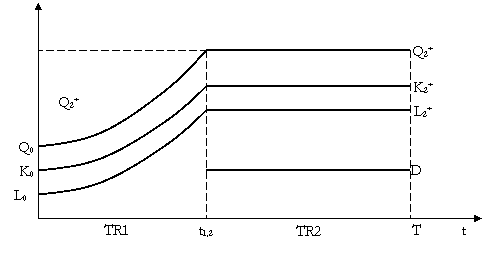
b) Daca c1 < c2 < c21 Þ magistrala TR1 TR3 TR4 TR5
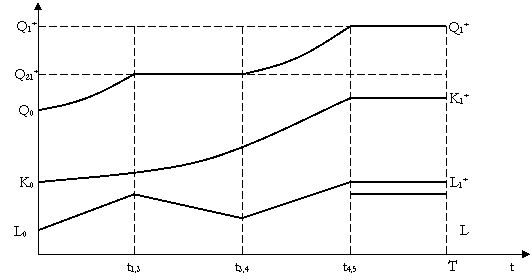
|
Politica de confidentialitate
|
Despre economie generala |
||||||||||
Stiu si altele ... |
||||||||||
|
||||||||||