
| MANAGEMENT
Termenul Management a fost definit de catre Mary Follet prin expresia "arta de a infaptui ceva impreuna cu alti oameni". Diferite informatii care te vor ajuta din domeniul managerial: Managementul Performantei, Functii ale managementului, in cariera, financiar. |
| StiuCum
Home » MANAGEMENT
» managementul productiei
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mecanisme ale comportamentului pe termen lung si pe termen scurt al producatorului |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mecanisme ale comportamentului pe termen lung si pe termen scurt al producatoruluiCadrul conceptualEvidentiem mecanismele decizionale privind: nivelul productiei nivelul factorilor ce trebuie utilizati penetrarea pe diverse piete Planuri de actiune: 1*) tehnologic: alegerea tehnologiilor in functie de: profilul productiei de resursele financiare de efectele progresului tehnic 2*) institutional-legislativ: deciziile trebuie sa se incadreze in normele legislative: pe plan financiar-economic protectia muncii (CAS) protectia mediului si mecanismele de piata: tipul concurentei (perfecta, i 131j97b mperfecta) piata bunurilor (produsul Q) piata capitalului piata fortei de munca piata valutara 3*) managerial: fundamentarea optima a deciziilor pe TS: aprovizionare productie desfacere si strategiilor pt TM si TL dezvoltarea firmei inputuri angajari personal Consecinte: In contextul concurential, trebuie sa formulam modele analitice (cibernetico-economice) pentru fundamentarea legitatilor de comportament optimal pe TS si TL al firmei. Conexiunile (fluxurile) cu ceilalti agenti economici (alte firme): furnizori si firme comerciale; cu consumatorii; cu institutiile financiare, bancare, guvernamentale; cu sectorul extern, sunt evidentiate prin tabloul de
operatiuni (tabloul de fluxuri si cel al activelor (active si pasive) ca
variabile de stare, reprezentate in modelul general al echilibrelor
macroeconomice, urmarind aici subsistemul “producatori” (sau “firme”), adica,
prin conventia de notatie folosita, multimea Principiul de analiza: este acelasi de la consumator, cel al unei firme reprezentative (Ipoteza Marshall). Analiza se diferentiaza dupa orizontul deciziei: pe
TS (cand capitalul pe
TL, cand capitalul Comportamentul pe TSPrincipii de analizaPrin ipoteza,
Decizia optima: vizeaza: nivelul
productiei al
angajarilor in functie de: costul
factorilor (aici salariul nominal brut pretul
de desfacere Modelul de baza il constituie functia de productie, care
cuantifica nivelul productiei Facem ipoteza ca productia este omogena si poate fi agregata
in indicatorul scalar
unde In mod curent, intrucat operam cu indicatorul valoarea
adaugata, singurul factor variabil pe care-l vom lua in specificarea modelului,
este forta de munca
unde indicele “ Consecinta: din (1’) se deduce ca cererea de munca este:
Determinarea functiei g este dependenta de: 10) tipul functiei de productie in raport cu caracteristica de substituibilitate (sau complementaritate a factorilor) 20) caracteristicile pietei de desfacere si de pozitia firmei pe aceasta piata (concurenta perfecta sau nu). 10) In raport cu prima caracteristica, avem doua variante de reprezentare: i) functia de productie cu factori complementari, prin care se reflecta stricta proportionalitate a factorilor, corespunzatoare randamentelor marginale constante ale lor:
unde, pe TS, capitalul este constant Deci Consecinta. Pe TS, functia de productie este:
Concluzii
unde
Deci orice angajare peste pragul Folosirea acestei functii de productie pentru optimizare va fi analizata in paragraful urmator in raport cu caracteristicile pietei bunurilor. ii) Opusa acestei situatii este reprezentarea functiei de productiei cu factori substituibili.
cu operatorul
si matricea hessiana negativ definita. Indicatorii de substituibilitate vor fi analizati in §……., cand folosim in modelare aceasta functie de productie. Dupa pozitia firmei pe piata, postulam 3 cazuri: a) Firma isi desfasoara activitatea in CCP (conditii de
concurenta perfecta); in consecinta nivelul preturilor (factorilor si de
desfacere), la noi b) Firma actioneaza in aceleasi conditii ca la a), adica
CCP, dar productia este limitata de absorbtia pietei c) Firma opereaza in conditii de concurenta imperfecta
(adica monopol sau oligopol – ca pozitie pe piata bunurilor, sau monopson,
monopol-monopson – ca pozitie pe piata factorilor). In conditii de monopol,
pretul de desfacere este fixat de firma Concluzie: obtinem 6 variante de analiza, dupa cum ne plasam intr-una din cele doua situatii tehnologice i) sau ii), combinata cu una din cele 3 situatii pe piata, a), b) sau c). De notat ca situatia c) se poate partitiona in variantele specifice concrete: monopol, duopol, oligopol etc. Analiza in cazul tehnologiei cu factori complementari si pozitiei de tip CCPDin functia de productie (1’’’.a) rezulta ca functia cererii de munca este:
Modelul de fundamentare a deciziei avand ca obiectiv
maximizarea proftlului
unde Tinand cont de functia cererii de munca (2’.a) rezulta ca volumul profitului brut este:
unde Observam ca functia profitului este liniara in raport cu
Decizia optima va fi:
unde Deci decizia depinde de productivitatea inregistrata Dar productivitatea Daca
Fundamentarea deciziei optime in conditiile tehnologiei cu complementaritatea factorilor si absorbtia limitata a pieteiPiata bunurilor este de tip CCP, deci
Cererea de forta de munca Decizia optima in conditii de concurenta imperfectaIn cazul firmei de monopol, pretul pietei este fixat tot de firma:
functia de profit este
unde functia de venituri este:
deci neliniara. Facem ipoteza ca Decizia asupra pretului Reactia consumatorului la pretul bunului, reflecta de regula
o evolutie a cererii de tip “S-intos”: cererea descreste mai intai lent pana la
un nivel
Functia de salarii este:
este de asemenea neliniara, monoton
crescatoare si convexa:
Aceste relatii reflecta conditionarile de optim, prin evidentierea corelatiilor intre variatia salariului total nominal si salariului (mediu) nominal orar, platit de firma. Decizia optima se obtine din modelul cibernetic (3’.c):
Conditia de ordin I:
Conditia de ordin II:
Dupa cum am precizat mai sus, Se observa ca exista doua situatii ((fig. 4.a) si (4.b)):
a) daca solutia optima a modelului (4.a),
b) daca optimul Nota: Prima situatie a) corespunde indicatorului
In consecinta, decizia optima privind oferta (productia) este:
si cererea de munca:
In concluzie, decizia optima de productie Decizia asupra pretului optim
adica
Si
Consecinte Din proprietatile functiei de
venit a) preturile fixate de firma sunt
descrescatoare: b) salariul nominal este crescator, Intr-adevar, din fig. 6 a) si b) deducem:
Avem:
Cum
Similar, din fig. 6.b, rezulta:
unde Aceste dinamici sunt generate de mecanismele celor doua piete: - pe piata bunurilor: (descresterea preturilor antreneaza cresterea cererii si
prin mecanism de ajustare a ofertei la cerere, cresterea ofertei - pe piata fortei de munca: Dinamica
cererii de forta de munca pe TS.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
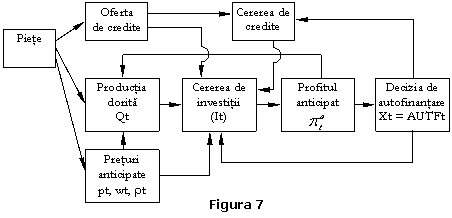 |
In mecanismul formarii cererii efective de
investitii, schema cibernetica este similara, dar conexiunile cu cele trei
piete: financiare (prin credite), a bunurilor si serviciilor si cea a fortei de
munca, evidentiaza si restrictiile anticipate privind volumul creditelor ![]() , volumul ofertei
, volumul ofertei ![]() in raport cu
capacitatea maxima
in raport cu
capacitatea maxima ![]() de absorbtie si
restrictia fortei de munca
de absorbtie si
restrictia fortei de munca ![]() .
.
Decizia de autofinantare evidentiaza dependente multiple prin:
![]() (12)
(12)
unde ![]() este “pretul net” de
desfacere pe unitatea de produs, obtinut prin deducerea din pretul de desfacere
a cheltuielilor cu factorii de productie ficsi (amortizarea capitalului) si cu
factorii variabili (consumuri intermediare), cu exceptia fortei de munca,
pentru care avem o specificare directa prin
este “pretul net” de
desfacere pe unitatea de produs, obtinut prin deducerea din pretul de desfacere
a cheltuielilor cu factorii de productie ficsi (amortizarea capitalului) si cu
factorii variabili (consumuri intermediare), cu exceptia fortei de munca,
pentru care avem o specificare directa prin ![]() ;
;
![]() - este volumul
dividendelor distribuite in anul
- este volumul
dividendelor distribuite in anul ![]()
![]() - volumul indatoririi
firmei la momentul
- volumul indatoririi
firmei la momentul ![]() prin creditele facute pana
la acest moment iar
prin creditele facute pana
la acest moment iar ![]() si
si ![]() reprezinta volumul rambursarilor
prin amortismentele anuale, respectiv dobanzile platite de firma, cu rata
dobanzii la credite
reprezinta volumul rambursarilor
prin amortismentele anuale, respectiv dobanzile platite de firma, cu rata
dobanzii la credite ![]() .
.
Ansamblul costurilor, cu factorii si a “costurilor de ajustare”, permite evaluarea rentabilitatii investitiei. Compararea cu indicatorul “rata q-marginala Tobin”, aduce in plus informatii privind interesul investitorilor pentru firma respectiva; modelul Tobin, folosit pe date statistice evidentiaza ca investitiile in firma respectiva sunt direct dependente de evolutia bursiera a firmei (“valoarea firmei”).
Acest mecanism, deosebit de important, pune in corelatie sursele de investitii, cu “rata q-marginala Tobin” si cu “efectul de levier”, in conditiile pietelor imperfecte. In litaratura de specialitate interconditionarile respective sunt facute prin cele doua toreme Modigliani-Miller (MMI si MMII), modele prezentate in paragraful 2.4, mai jos.
In cadrul
conceptual prezentat mai sus, ne plasam intr-o dinamica cu doua perioade t si ![]() , reflectand prezentul respectiv viitorul. Aceasta abordare
nu diminueaza validitatea specificarii modelului, extinderea facandu-se similar
pentru
, reflectand prezentul respectiv viitorul. Aceasta abordare
nu diminueaza validitatea specificarii modelului, extinderea facandu-se similar
pentru ![]() perioade, dar simplifica
calculatia, permitand formularea cu usurinta a legitatilor de comportament ce
se desprind din modelarea acestor mecanisme de reglare.
perioade, dar simplifica
calculatia, permitand formularea cu usurinta a legitatilor de comportament ce
se desprind din modelarea acestor mecanisme de reglare.
In aceasta viziune, variabilele din perioada prezenta sunt presupuse observabile:
- productia: Qt – cunoscuta, evaluata la pretul pt - cunoscut;
-
factorii de productie: Kt
– capitalul si Nt – forta
de munca, evaluate la preturile ![]() respectiv wt – cunoscute.
respectiv wt – cunoscute.
Variabilele
viitoare: ![]() si preturile asteptate
si preturile asteptate
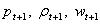 - sunt variabile
anticipate.
- sunt variabile
anticipate.
Decizia
de investitii ![]() se fundamenteaza pe
nivelul dorit al capacitatilor, exprimate prin stocul dorit de capital
se fundamenteaza pe
nivelul dorit al capacitatilor, exprimate prin stocul dorit de capital ![]() , in functie de coeficientul de depreciere a capitalului
(vezi (11’)):
, in functie de coeficientul de depreciere a capitalului
(vezi (11’)):
![]() (11’.b)
(11’.b)
Profitul total actualizat asteptat (pe cele doua perioade) va fi:
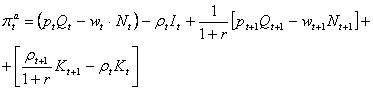 (13)
(13)
si evidentiaza 4 componente:
- primul termen este profitul brut in perioada de baza t;
-
al 2-lea, cuantifica cheltuielile de investitii facute in perioada de baza, la
costul de oportunitate ![]() al capitalului in
aceasta perioada;
al capitalului in
aceasta perioada;
-
al 3-lea este profitul brut anticipat pentru perioada urmatoare, actualizat cu
factorul de scont ![]() ;
;
-
al 4-lea este plusvaloarea stocului de capital actualizat, prin reevaluare la
noile costuri ![]() , ca urmare a inflatiei asteptate
, ca urmare a inflatiei asteptate ![]() pe piata bunurilor de capital.
pe piata bunurilor de capital.
Pentru
simplificarea notatiilor notam ![]() , perioada de baza si
, perioada de baza si ![]() , perioada viitoare. Inlocuind
, perioada viitoare. Inlocuind ![]() in ecuatia profitului
in ecuatia profitului ![]() , si regrupand, deducem:
, si regrupand, deducem:
![]() (13’)
(13’)
unde ![]() este costul asteptat al capitalului,
este costul asteptat al capitalului,
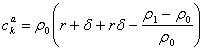 (14)
(14)
Observatii daca rata dobanzii r este mica (4-8%), termenul ![]() este neglijabil (de
exemplu pentru
este neglijabil (de
exemplu pentru ![]() , gasim
, gasim ![]() ‰, neglijabil, daca operam cu doua zecimale exacte); din
acest motiv, in majoritatea lucrarilor de specialitate, pentru costul asteptat
al capitalului se foloseste indicatorul
‰, neglijabil, daca operam cu doua zecimale exacte); din
acest motiv, in majoritatea lucrarilor de specialitate, pentru costul asteptat
al capitalului se foloseste indicatorul
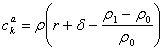 (14’)
(14’)
care evidentiaza un indice de
crestere a costului de oportunitate al capitalului, ![]() , cu
, cu ![]() , dat de nivelul ratei dobanzii r, al ratei deprecierii δ
si de rata inflatiei asteptate
, dat de nivelul ratei dobanzii r, al ratei deprecierii δ
si de rata inflatiei asteptate ![]() .
.
Acest cost actioneaza ca un mecanism feed-back negativ asupra profitului asteptat, interpretarea economica fiind:
-
utilizarea viitoare a unei unitati de capital ![]() la valoarea
la valoarea ![]() (lei/u.K.),
investitorul pierde suma
(lei/u.K.),
investitorul pierde suma ![]() reprezentand dobanda
pe care ar fi primit-o prin plasament in banci (sau in titluri), sau
echivalent, plateste aceasta dobanda la imprumutul pentru obtinerea acestei
u.K.;
reprezentand dobanda
pe care ar fi primit-o prin plasament in banci (sau in titluri), sau
echivalent, plateste aceasta dobanda la imprumutul pentru obtinerea acestei
u.K.;
-
prin depreciere, u.K. pierde din valoare suma ![]() ;
;
-
cresterea preturilor bunurilor de capital (inflatia) aduce un castig prin
reevaluare, egal cu ![]() aceasta componenta
reliefeaza comportamentul agentilor economici de a investi in bunuri de capital
atunci cand inflatia asteptata este mare.
aceasta componenta
reliefeaza comportamentul agentilor economici de a investi in bunuri de capital
atunci cand inflatia asteptata este mare.
Criteriul de optim este maximizarea profitului actualizat
sub restrictiile de incadrare a productiei realizate ![]() si
si ![]() in volumul admisibil,
dat de functia de productie a firmei:
in volumul admisibil,
dat de functia de productie a firmei:
![]() si
si ![]() (15)
(15)
Problema se modifica prin restrictiile induse de diverse piete, atunci cand obiectivul este cererea efectiva de investitii.
Formularea problemei:
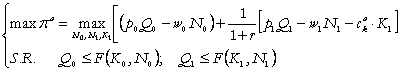 (15)
(15)
Se descompune in doua probleme independente:
 Þ decizia optima
Þ decizia optima ![]() (16)
(16)
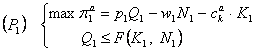 Þ decizia optima
Þ decizia optima ![]() (17)
(17)
Din ![]() se deduce investitia
ce trebuie facuta la momentul 0:
se deduce investitia
ce trebuie facuta la momentul 0:
![]() (11’’)
(11’’)
Functionarea acestui mecanism de reglare dinamica optimala se fundamenteaza pe principiul descompunerii intertemporale, structurat ca sistem ierarhic pe doua nivele (figura 8).
![]()
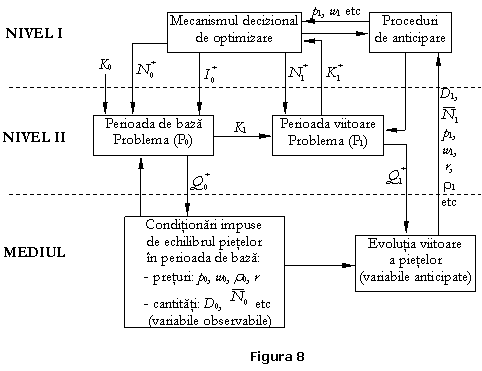
Aceasta schema cibernetica sintetica evidentiaza rolul mediului (politico-economic, social, ecologic, cadrul legislativ, etc.) prin echilibrele (dezechilibrele) pietelor si evolutia anticipata a acestora, in fundamentarea deciziilor firmei precum si a corectitudinii anticiparilor facute de firma asupra acestor evolutii. Prezentarea analitica a multitudinii de conexiuni se face evidentiind fiecare variabila si interdependentele dintre acestea prin procedurile de specificare cunoscute, bazate pe metoda cutiei negre (tema – propunem reprezentarea cat mai detaliata de catre cititor).
Vizeaza doi indicatori:
- politica de personal ![]()
- decizia de investitii ![]() ,
,
volumul productiei ![]() fiind variabila de
iesire.
fiind variabila de
iesire.
Decizia de investitii ![]() va fi insa rezultatul
optimizarii pe TL, prin rezolvarea modelului
va fi insa rezultatul
optimizarii pe TL, prin rezolvarea modelului ![]() .
.
Ramane numai variabila ![]() care se deduce din
rezolvarea modelului
care se deduce din
rezolvarea modelului ![]() , intrucat K0 este
dat si in consecinta perioada de baza t
= 0 este echivalenta cu ceea ce in paragraful 2.2.5 am numit TS.
, intrucat K0 este
dat si in consecinta perioada de baza t
= 0 este echivalenta cu ceea ce in paragraful 2.2.5 am numit TS.
Deosebirea consta in
forma de specificare a functiei de productie, ![]() , care, in acest caz este cu factori substituibili, deci are
proprietatile cunoscute din microeconomie, reflectand cerintele legitatii
randamentelor marginale descrescatoare ale factorilor si corelatiile necesare
intre aceste randamente induse de conditia ca matricea hessiana HF sa fie negativ
(semi)definita.
, care, in acest caz este cu factori substituibili, deci are
proprietatile cunoscute din microeconomie, reflectand cerintele legitatii
randamentelor marginale descrescatoare ale factorilor si corelatiile necesare
intre aceste randamente induse de conditia ca matricea hessiana HF sa fie negativ
(semi)definita.
In aceste conditii,
rezolvarea problemei ![]() se face, observand ca
exista doua situatii:
se face, observand ca
exista doua situatii:
a) Cererea pietei ![]() este mult mai mare
decat oferta firmei la capacitatea maxima de productie; deci conditionarile
pietei bunurilor nu sunt efective.
este mult mai mare
decat oferta firmei la capacitatea maxima de productie; deci conditionarile
pietei bunurilor nu sunt efective.
Modelul ![]() devine:
devine:
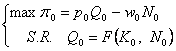 (16.a)
(16.a)
adica:
![]() ,
,
de unde, prin CNO, deducem:
![]()
![]()
si in consecinta decizia optima**) este:
![]()
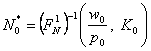 (16’.a)
(16’.a)
care evidentiaza dependenta cererii
de forta de munca de capitalul disponibil (pe TS), K0 si de costul relativ al muncii ![]() .
.
Consecinta: Cum ![]() este descrescatoare,
este descrescatoare, ![]() este de asemenea
descrescatoare si deci:
este de asemenea
descrescatoare si deci:
![]()
![]()
![]()
![]() Þ
Þ ![]() Þ
Þ ![]()
unde productia realizata este:
![]() .
.
b)
Daca oferta firmei la capacitatea maxima de productie depaseste cererea ![]() atunci oferta va fi:
atunci oferta va fi: ![]() , deci
, deci ![]() si decizia optima este
si decizia optima este
![]() (16’.b)
(16’.b)
adica, cererea de munca este dependenta in sens direct de absorbtia pietei:
![]()
![]()
![]()
![]() Þ
Þ ![]() Þ
Þ ![]()
(deoarece ![]() unde F -1 este monoton
crescatoare in raport cu
unde F -1 este monoton
crescatoare in raport cu ![]() ).
).
Dupa cum am definit in § 2.3.1.1 cererea potentiala de investitii nu este conditionata de restrictiile impuse de piata bunurilor, piata muncii, piata capitalului etc.
Decizia asupra investitiei ce trebuie facuta in perioada de
baza pentru dezvoltarea viitoare a firmei este fundamentata pe modelul ![]() , care in aceste conditii, devine
, care in aceste conditii, devine
![]() (17.a)
(17.a)
deoarece ![]() , restrictiile de conditionare nefiind efective. Deducem
(CNO):
, restrictiile de conditionare nefiind efective. Deducem
(CNO):
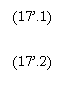
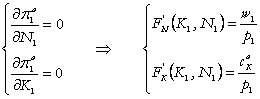
sistem, prin rezolvarea caruia gasim deciziile optime :
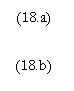
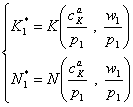
care evidentiaza dependenta de
costurile relative anticipate ale capitalului ![]() si muncii
si muncii ![]() .
.
Analiza efectelor modificarii acestor costuri se face prin diferentierea (CNO); deducem,
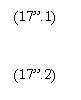
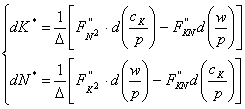
unde ![]() .
.
Cum ![]() se constata ca efectul
direct al cresterii costurilor relative ale celor doi factori este descresterea
capitalului, respectiv al personalului.
se constata ca efectul
direct al cresterii costurilor relative ale celor doi factori este descresterea
capitalului, respectiv al personalului.
Cum, de regula ![]() , efectul cresterii concomitente a costurilor relative a
celor doi factori este cert si anume descresterea volumului de factori.
Proportiile cresterilor respective sunt date de raportul intre derivatele de
ordin doi si determinantul matricei hessiene.
, efectul cresterii concomitente a costurilor relative a
celor doi factori este cert si anume descresterea volumului de factori.
Proportiile cresterilor respective sunt date de raportul intre derivatele de
ordin doi si determinantul matricei hessiene.
De
exemplu, cresterea salariului real ![]() cu o unitate
antreneaza o descrestere a capitalului cu
cu o unitate
antreneaza o descrestere a capitalului cu ![]() unitati si a muncii,
cu
unitati si a muncii,
cu ![]() , ore.
, ore.
Observatii
1. In aceasta analiza, mai importanta este evidentierea procentuala a acestor efecte, care se face prin introducerea elasticitatilor cererii de capital si de munca in raport cu costurile relative anticipate ale lor, notate:
![]()
si elasticitatile incrucisate:
![]()
unde ![]() reprezinta variatia
(cresterea, descresterea) variabilei x.
reprezinta variatia
(cresterea, descresterea) variabilei x.
Nota
a) Cunoscand functiile de cerere de factori (18.a), (18.b) aceste elasticitati se determina prin formulele echivalente:
![]() , etc.
, etc.
b) Din analiza facuta mai sus asupra sensului variatiilor rezulta ca aceste elasticitati sunt negative.
Astfel, deducem ca o
crestere a salariului real ![]() cu 1% induce o
descrestere a capitalului cu
cu 1% induce o
descrestere a capitalului cu
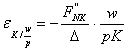 %
%
Similar, pentru celelalte efecte.
2. Adancirea analizei se poate face prin evidentierea variatiei diverselor “preturi”:
Astfel, variatia costului
relativ al capitalului, 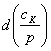 , va reflecta ritmurile de crestere
al costului capitalului,
, va reflecta ritmurile de crestere
al costului capitalului, ![]() si preturilor
si preturilor ![]() , prin relatia
, prin relatia
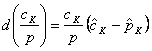 (14’.a)
(14’.a)
Intr-adevar, 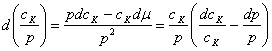
Similar pentru variatia
salariului real ![]() ,
,
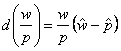
Se evidentiaza astfel cum
se modifica cererea de factori nu numai in functie de costurile reale ale
factorilor 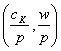 ci si de ritmurile
cresterii lor
ci si de ritmurile
cresterii lor ![]() si ale preturilor
si ale preturilor ![]() .
.
Studii de caz. Identificati functiile de
cerere de factori. ![]() si de investitii
si de investitii ![]() si analizati efectele
modificarii costurilor relative asupra acestor decizii, cand functia de
productie este:
si analizati efectele
modificarii costurilor relative asupra acestor decizii, cand functia de
productie este:
10) Cobb-Douglas, ![]()
20) CFS: ![]()
cu ![]()
Daca functia de productie pentru firma analizata este cu randamente constante la scala, suma elasticitatilor productiei in raport cu factorii este egala cu unitatea:
![]()
sau echivalent, gradul de omogenitate al
functiei de productie este 1. In acest caz functia de productie poate fi
specificata prin indicatorul ![]() - inzestrarea tehnica
a muncii, prin relatia
- inzestrarea tehnica
a muncii, prin relatia
![]()
unde ![]() este productivitatea
(aici orara) a muncii.
este productivitatea
(aici orara) a muncii.
Tinand seama ca productivitatea marginala a muncii si randamentul marginal al capitalului au expresiile:
![]()
si:
![]() ,
,
conditiile necesare de optim (17’.1) si (17’.2) devin
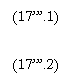

sistem cu o singura necunoscuta ![]() , deci in general incompatibil.
, deci in general incompatibil.
Daca folosim prima ecuatie, deducem:
(17’’’.a)
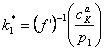
care defineste proportia optima intre capital si munca ce trebuie folosita de firma in viitor; este admisibila daca salariul real platit de firma este :
(17’’’.b)
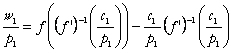
Importanta in aceasta analiza este teorema Euler pentru functii omogene (teorema Euler 1, a gradientului), care se scrie aici:
![]()
Cum la optim (din (17.’1), (17.’.2)) avem:
![]() ,
,
din teorema Euler rezulta ca:
![]()
Din ![]() , deducem:
, deducem:
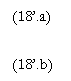
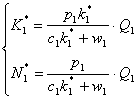
deci cererea de factori este
proportionala cu nivelul ![]() , al productiei, care nu poate fi determinat endogen ci este
fixata de firma. Corespunzator, cererea de investitii este
, al productiei, care nu poate fi determinat endogen ci este
fixata de firma. Corespunzator, cererea de investitii este
(18’.c)
![]()
care arata ca este liniar dependenta de nivelul anticipat al productiei si care ne atrage atentia asupra similitudinii cu mecanismul accelerator (vezi paragraful urmatot).
Studiu de caz. Formulati mecanismul decizional al reglarii dinamice optimale pentru o firma a carei functie de productie a fost identificata ca fiind cu randamente constante la scala:
a) tip Cobb-Douglas: ![]()
b) tip CES ( cu ![]() ),
), ![]()
Indicatie: Gasim expresia productivitatii muncii, in cazul:
a) ![]() b)
b) ![]()
diferenta intre ele constand in faptul ca in primul caz evolutia productivitatii este crescatoare, concava, neplafonata, iar in al 2-lea caz este plafonata.
In cazul (a) gasim nivelul optim al inzestrarii tehnice
asteptate pentru perioada viitoare: 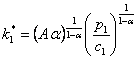 .
.
In consecinta, nivelul capitalului pentru perioada viitoare va fi:
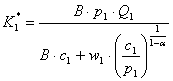 ,
,
unde![]() .
.
Similar pentru cazul b).
Restrictii anticipate asupra capacitatii de absorbtie a pietei
Producatorul anticipeaza nivelul viitor al absorbtiei
pietei, ![]() si isi propune sa
acopere aceasta cerere, adica sa opereze la nivelul de scala
si isi propune sa
acopere aceasta cerere, adica sa opereze la nivelul de scala 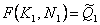 . Modelul de optimizare devine acum:
. Modelul de optimizare devine acum:
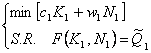 (19)
(19)
Conditiile necesare de optim sunt aceleasi ca si in cazul maximizarii profitului asteptat: proportionalitatea randamentelor marginale cu costurile asteptate; prin eliminarea multiplicatorului Lagrange se deduce sistemul:
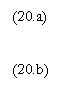
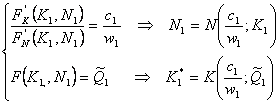
deci cererea de factori este dependenta
de nivelul productiei anticipate si de costul anticipat ![]() al celor doi factori.
al celor doi factori.
In consecinta, cererea de investitii este:
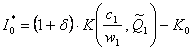
Insa ![]() s-a fundamentat
printr-o metodologie similara la momentul
s-a fundamentat
printr-o metodologie similara la momentul ![]() , adica
, adica 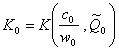 . Se obtine modelul general al cererii de investitii.
. Se obtine modelul general al cererii de investitii.
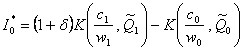 (21)
(21)
prin care generalizam modelul de tip accelerator in formarea cererii de investitii.
![]() (22)
(22)
unde ![]() si
si ![]() este coeficientul
capitalului,
este coeficientul
capitalului, ![]() .
.
Comparatia directa intre modelul general (21) si modelul
accelerator (22) este posibila in cazul cel mai simplu cand capitalul dorit ![]() descris prin functia
(20.b) este liniar in raport cu productia
anticipata
descris prin functia
(20.b) este liniar in raport cu productia
anticipata ![]() , adica:
, adica:
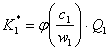 (23)
(23)
Se obtine:
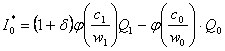 (21’)
(21’)
si daca ![]() este aproximativ
constant, se deduce:
este aproximativ
constant, se deduce:
![]() (22’)
(22’)
relatia care evidentiaza mecanismul
accelerator prin investitia neta ![]() la care se adauga
investitia de recuperare a capitalului depreciat
la care se adauga
investitia de recuperare a capitalului depreciat ![]() .
.
Ipoteza liniaritatii capitalului necesar, cu nivelul productiei dorite nu este intamplatoare: ea se regaseste in toate modelele in care functia de productie este cu randamente constante la scala, asa cum am evidentiat in §2.3.2.3.
Astfel din relatia (18’.c), deducem ca acceleratul ![]() este:
este:
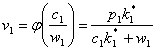 (23’)
(23’)
si daca ratele de crestere ale costurilor
factorilor sunt aceleasi cu rata inflatiei 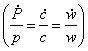 , se constata ca
, se constata ca ![]() este constant.
este constant.
Asadar, pentru functia de productie Coob Douglas cu randamente constante de scala, modelul accelerator al investitiei este:
![]()
si in ipoteza indexarii perfecte a costurilor cu rata inflatiei, avem:
![]()
Studii de caz
1. Reformulati problema mecanismulului accelerator cand
indexarile nu sunt perfecte. Determinati acceleratorul investitiilor ![]() daca rata de indexare
a salariilor in raport cu inflatia este
daca rata de indexare
a salariilor in raport cu inflatia este ![]() ; pentru costul capitalului se vor folosi relatiile (14) si
(14’).
; pentru costul capitalului se vor folosi relatiile (14) si
(14’).
2. Aplicati rezultatele obtinute pentru functiile a), b) din studiul de caz din paragraful anterior.
Observatii Mecanismul accelerator evidentiaza o reactie puternica (chiar violenta) a investitiei la cresterea productiei.
Astfel, pentru doua proiecte de investitii ![]() care ar permite
cresterea productiei cu ratele
care ar permite
cresterea productiei cu ratele ![]() , respectiv r2 fata de
, respectiv r2 fata de ![]() (cu
(cu ![]() ), ritmul de crestere a investitiei este:
), ritmul de crestere a investitiei este:
![]()
si se observa ca este independent de accelerator.
Numeric, daca ![]() , deci cresterea productiei cu o rata de 2% antreneaza o crestere a
investitiei de aproximatie 20%, deci un efort considerabil.
, deci cresterea productiei cu o rata de 2% antreneaza o crestere a
investitiei de aproximatie 20%, deci un efort considerabil.
Mecanismul de descompunere la doua nivele folosit in fundamentarea deciziei a permis determinarea unui indicator complex, care este costul anticipat al capitalului (vezi relatia (14)). Problema este insa foarte complexa intrucat introducerea costurilor de ajustare ale capitalului afecteaza valoarea de piata a firmei si increderea investitorilor in plasamente in aceasta firma. Se face astfel legatura cu teoria “ratei q-Tobin” care face conexiunea intre decizia de investitii a firmei cu piata valorilor mobiliare ca sursa de finantare.
Costurile de
ajustare – se
pot specifica prin costurile induse de realizarea investitiei, exclusiv
valoarea investitiei in bunuri de capital ![]() ; aceste costuri sunt contabilizate prin cheltuielile de
proiectare, de creere a infrastructurii (drumuri de acces, utilitati necesare
constructorilor, etc.). Notam aceste costuri cu
; aceste costuri sunt contabilizate prin cheltuielile de
proiectare, de creere a infrastructurii (drumuri de acces, utilitati necesare
constructorilor, etc.). Notam aceste costuri cu ![]() si introducem ipoteza,
conform validarilor empirice, ca aceasta functie este functia convexa (fig. 9)
si verifica cerintele:
si introducem ipoteza,
conform validarilor empirice, ca aceasta functie este functia convexa (fig. 9)
si verifica cerintele:
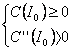 (23)
(23)
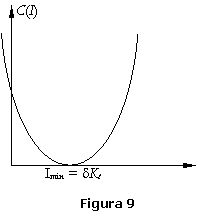
cu un minim in ![]() in cazul ca se
foloseste indicatorul
in cazul ca se
foloseste indicatorul ![]() - investitii nete, sau
minimul este
- investitii nete, sau
minimul este ![]() in cazul cand se
foloseste indicatorul
in cazul cand se
foloseste indicatorul ![]() = investitii brute,
aceasta ultima cerinta evidentiind faptul ca firma trebuie sa asigure cel putin
investitia de recuperare
= investitii brute,
aceasta ultima cerinta evidentiind faptul ca firma trebuie sa asigure cel putin
investitia de recuperare ![]() a capitalului
depreciat
a capitalului
depreciat ![]() . Ramura crescatoare reflecta cresterea convexa a acestor
costuri indusa de volumul investitiei realizate; ramura descrescatoare
evidentiaza procesul invers, de dezinvestitii (decapitalizare) prin pierderile
inregistrate.
. Ramura crescatoare reflecta cresterea convexa a acestor
costuri indusa de volumul investitiei realizate; ramura descrescatoare
evidentiaza procesul invers, de dezinvestitii (decapitalizare) prin pierderile
inregistrate.
Profitul actualizat asteptat va fi influentat de aceste
costuri de ajustare si se obtine din expresia ![]() scazand
scazand ![]() .
.
Obtinem indicatorul “valoarea firmei”:
 (24)
(24)
Modelul de optimizare dinamica devine:
![]()
Lagrangeanul:
![]() (24’)
(24’)
unde, multiplicatorul Lagrange ![]() are interpretarea
cunoscuta:
are interpretarea
cunoscuta:
![]()
adica “pretul umbra” al investitiei:
cresterea valorii ![]() a firmei, la cresterea
cu o unitate a volumului investitiei.
a firmei, la cresterea
cu o unitate a volumului investitiei.
Indicatorul ![]() - adica valoarea reala a cresterii marginale a
valorii optime a firmei se numeste rata
q-marginala Tobin: Determinarea concreta
- adica valoarea reala a cresterii marginale a
valorii optime a firmei se numeste rata
q-marginala Tobin: Determinarea concreta
rezulta din ![]() :
:

Asadar, daca indicele de crestere a costului capitalului
este acelasi cu cel al preturilor (adica ![]() ), atunci rata q-marginala Tobin este data de costul marginal
de ajustare a investitiilor plus 1.
), atunci rata q-marginala Tobin este data de costul marginal
de ajustare a investitiilor plus 1.
Rezulta ca investitia optima este:
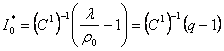
unde, din ecuatia a doua deducem![]() :
:
![]() (daca
(daca
![]() )
)
si deci din prima ecuatie, obtinem
cererea de munca ![]() .
.
In practica, indicatorul folosit este rata q-media Tobin:
![]() , deci nu este necesara expresia analitica
, deci nu este necesara expresia analitica ![]() .
.
Aceasta decizie, are la baza teorema:
Teorema: Daca functia de productie este
cu randamente constante la scala, in
conditiile pietelor perfect concurentiale,
atunci ![]() .
.
Demonstratia: Folosim proprietatea Euler pentru functii
omogene de grad 1, ![]() si inlocuim
si inlocuim ![]() in expresia ratei
in expresia ratei ![]() , dupa amplificarea cu
, dupa amplificarea cu ![]() . Obtinem in final,
. Obtinem in final, ![]() .
.
Studiu de caz: Pentru functia ![]() , formulati modelul de mai sus corespunzator functiilor de
productie Cobb Douglas si CES in cele doua variante:
, formulati modelul de mai sus corespunzator functiilor de
productie Cobb Douglas si CES in cele doua variante:
V1) cu randamente constante de scala
V2) cu randamente descrescatoare
si fundamentati decizia optima, evidentiind corelatia cu rata q-Tobin.
In paragrafele anterioare am evidentiat formarea cererii de investitii. Punem acum problema finantarii acestor investitii: care este raportul optim intre sursele proprii (autofinantarea) si sursele atrase (imprumuturi)?
Modelul a fost formulat de Miller si Modigliani, initial (in 1958) in conditiile pietelor financiare perfecte (PFP) apoi dezvoltat (1963), cand pietele sunt imperfecte (PFI).
Rezultatele sunt cunoscute in literatura de specialitate prin teorema MM1, respectiv MM2, prescurtare de la Miller-Modigliani.
Teorema MM1: In conditiile PFP, modul de finantare a investitiilor este fara importanta.
Spunem ca in aceste conditii avem o “neutralitate” in sens MM a deciziei optime de finantare a investitiilor firmei.
Deci exista neutralitate intre cele doua surse:
- imprumuturi: emisiune de obligatiuni sau apelarea la credite
- emisiunea de actiuni (autofinantare), cand firma apeleaza la proprietarii ei, pentru suplimentarea capitalului social al firmei
Intr-adevar, in conditiile PFP, la echilibru, toate formele de plasament au randamente egale (dupa corectia riscului, asa cum se stie din “teoria portofoliilor”).
Notam B – volumul imprumuturilor si ![]() - rata de levier,
definita prin ponderea imprumuturilor in capitalul detinut.
- rata de levier,
definita prin ponderea imprumuturilor in capitalul detinut.
Cum randamentele sunt egale, cresterea venitului actualizat asteptat va fi aceeasi fie ca pentru investitii se folosesc imprumuturi pe piata financiar-bancara, fie prin vanzare-cumparare de actiuni, cu acelasi risc.
Teorema MM2. In conditiile PFI, firma face
investitii intr-o structura de finantare data de rata maxima de levier, ![]() , deci la volumul maxim posibil al imprumuturilor, in
conditiile existente.
, deci la volumul maxim posibil al imprumuturilor, in
conditiile existente.
Imperfectiunea pietelor financiare este indusa de mai multi factori:
- politicile fiscale (legislatia fiscala): dobanzile platite la imprumuturi (r·B) sunt deductibile din baza de impozitare, fata de actiuni, unde dividendele distribuite nu sunt deductibile, ceea ce creaza imperfectiunea intre piata obligatiunilor si cea a actiunilor, si nu mai exista neutralitatea privind raportul imprumuturi/surse proprii;
- imperfectiunea pietelor financiare este generata si de cadrul sistemului de fiscalitate: impozitarea firmelor si cea a gospodariilor, este diferita (aspect studiat de Miller – vezi § 2.4.3);
- existenta riscului de faliment: - creditorii nu-si mai pot primi imprumuturile facute si dobanzile la acestea; rezulta ca imprumuturile (B) si autofinantarile (AUTF) nu mai sunt perfect substituibile;
- asimetria informatiei, reflectata prin mecanismul de semnalizare intre diverse grupuri de interese (interside-outsider);
- aversiunea diferita fata de risc a managerilor;
- tensiuni intre manageri si actionari, intre actionari si creditori, etc.
Teorema MM2, in conditiile impuse prin
mecanismele sistemului fiscal, se demonstreaza pornind de la criteriul maximizarii valorii nete actualizate a firmei,
coeficientul de actualizare fiind ![]() si rata (medie) de
impozitare fiind
si rata (medie) de
impozitare fiind ![]() ; se obtine modelul:
; se obtine modelul:

expresia din paranteza dreapta
reprezentand profitul net, dupa
achitarea impozitului pe profit din care se deduce dobanda la credite, ![]() si achitarea
datoriilor
si achitarea
datoriilor ![]() si a serviciului
datoriei
si a serviciului
datoriei ![]() .
.
Putem scrie:
![]()
 Constatam ca
Constatam ca ![]() , deci cu cat imprumuturile sunt mai mari cu atat este mai
mare valoarea cotatiei bursiere a firmei:
, deci cu cat imprumuturile sunt mai mari cu atat este mai
mare valoarea cotatiei bursiere a firmei: ![]() . Exista insa o valoare maxima al levierului,
. Exista insa o valoare maxima al levierului, ![]() , dat de acel nivel care anuleaza
efectul de fiscalitate:
, dat de acel nivel care anuleaza
efectul de fiscalitate:
![]()
Notand ![]() - rata profitului,
gasim:
- rata profitului,
gasim:
![]() - adica raportul intre
rata profitului si rata dobanzii la credite.
- adica raportul intre
rata profitului si rata dobanzii la credite.
Costul unitar al capitalului – in functie de levier, se identifica in mod similar prin demersul folosit in calculatia bazata pe profitul actualizat anticipat (vezi § 2.3.1.3).
In varianta analizata mai sus, nu am tinut cont de inflatie;
daca scriem valoarea neta actualizata tinand seama de preturile ![]() ale perioadei de
baza respectiv ale perioadei viitoare,
obtinem:
ale perioadei de
baza respectiv ale perioadei viitoare,
obtinem:

unde ![]() este volumul
imprumuturilor.
este volumul
imprumuturilor.
Grupand si notand ![]() , unde
, unde ![]() este rata anticipata a
inflatiei, deducem:
este rata anticipata a
inflatiei, deducem:
![]() (14”)
(14”)
deoarece ![]() .
.
Se constata similitudinea cu costul anticipat al capitalului
![]() dat de relatia (14)’,
dar acum apare in plus termenul
dat de relatia (14)’,
dar acum apare in plus termenul ![]() , ca efect al fiscalitatii.
, ca efect al fiscalitatii.
Analizam comportamentul optimal dinamic, pe 2 perioade.
Formulam un model cibernetic structurat in 4 subsisteme:
I) Subsistemul
producatorilor (firmele) cuprinzand multimea lor ![]() care isi finanteaza
investitiile
care isi finanteaza
investitiile ![]() , in perioada de baza
, in perioada de baza ![]() , apeland la una sau alta din sursele:
, apeland la una sau alta din sursele:
a) prin emisiune de obligatiuni (deci imprumuturi) ![]() la rata de randament
la rata de randament ![]() ;
;
b) prin emisiune de actiuni, in volum ![]() .
.
Valoarea bursiera a firmei este ![]() in perioada de baza.
in perioada de baza.
Excedentul ![]() este distribuit ca
dividende actionarilor, proportional cu cota parte
este distribuit ca
dividende actionarilor, proportional cu cota parte ![]() detinuta de actionarul
i la firma j la inceputul perioadei
detinuta de actionarul
i la firma j la inceputul perioadei ![]() .
.
II) Subsistemul
gospodariilor (consumatorii) contine multimea gospodariilor ![]() , care decid asupra plasamentului economiilor lor, in:
, care decid asupra plasamentului economiilor lor, in:
a) obligatiuni, in volum ![]() ;
;
b) actiuni la firma j,
in volum ![]() , unde
, unde ![]() este cota parte a
actiunilor detinuta la firma j a
gospodariei i la sfarsitul perioadei
este cota parte a
actiunilor detinuta la firma j a
gospodariei i la sfarsitul perioadei ![]() . Volumul total al plasamentelor in actiuni al gospodariei i este:
. Volumul total al plasamentelor in actiuni al gospodariei i este:
![]()
Obs Gospodaria i este deja proprietara cotei parti ![]() din valoarea firmei in
perioada anterioara;
din valoarea firmei in
perioada anterioara;
c) lichiditati plasate in banci, cu rata dobanzii ![]() , in volum
, in volum ![]() .
.
Ecuatia bugetului gospodariei i in perioada de baza este:
![]()
unde ![]() este consumul
gospodariei i in perioada
este consumul
gospodariei i in perioada ![]() .
.
![]() - sunt veniturile non
financiare ale gospodariei i.
- sunt veniturile non
financiare ale gospodariei i.
III) Subsistemul fiscal – actioneaza prin:
- rata impozitului pe profitul firmelor, rata unica t
- rata impozitului pe proprietatea gospodariei Fi, ti
- dividendele nu sunt impozitabile (aceasta ipoteza se bazeaza pe principiul neadmisibilitatii dublei impozitari, intrucat dividendele au fost impozitate la firma).
IV Pietele financiar-bancare: opereaza cu:
- rata dobanzii bancare si la titlurile (bonuri)
guvernamentale pentru atragerea lichiditatilor, ![]() ;
;
- rata de randament la obligatiuni: r.
De regula ![]() .
.
Se obtine schema cibernetica din fig.10, care evidentiaza pe langa conexiunile dintre cele 4 subsisteme si blocul de optimizare dinamica.
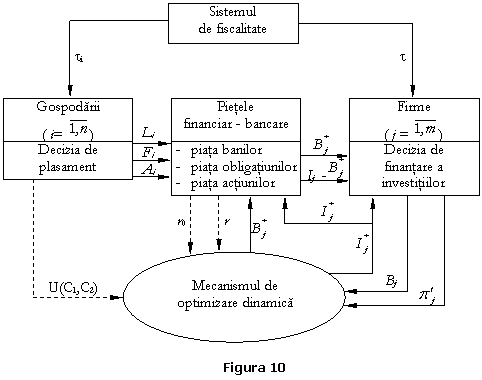
Pe baza investitiei facute ![]() in perioada de baza,
firma anticipeaza profitul perioadei urmatoare,
in perioada de baza,
firma anticipeaza profitul perioadei urmatoare, ![]() si volumul de
dividende ce va fi distribuit, dupa plata impozitelor,
si volumul de
dividende ce va fi distribuit, dupa plata impozitelor, ![]() , catre actionari, proportional cu cota
, catre actionari, proportional cu cota ![]() de actiuni detinute.
de actiuni detinute.
In aceste conditii, consumul din perioada 1 al gospodariei i va fi:
![]()
Nota Modelul poate fi extins la T perioade.
Tema: formulati modelul cand T = 3; in acest caz pentru perioada ![]() , ecuatia de buget va fi identica cu cea pentru perioada 0,
dar cu indicele de timp
, ecuatia de buget va fi identica cu cea pentru perioada 0,
dar cu indicele de timp ![]() , in loc de
, in loc de ![]() ; pentru perioada
; pentru perioada ![]() , ecuatia consumului va fi similara cu cea pentru
, ecuatia consumului va fi similara cu cea pentru ![]() de mai sus, dar cu
indicele 2.
de mai sus, dar cu
indicele 2.
Mecanismul de optimizare
A. Mecanismul de
optimizare pentru consumatori: consumatorul i maximizeaza functia proprie de utilitate ![]() .
.
Scriem pentru simplificare ![]() , unde
, unde ![]() si
si ![]() si inlocuim in
si inlocuim in ![]() expresiile lor:
expresiile lor:
![]()
si ![]() - cu expresia de mai
sus.
- cu expresia de mai
sus.
Din modelul ![]() , deducem cele trei CNO.
, deducem cele trei CNO.
![]()
prin care se fundamenteaza decizia optima
de plasament ![]() .
.
10) Prima conditie se scrie:
![]()
adica
![]()
deci RMS intre ![]() si
si ![]() trebuie sa fie egala
cu r0.
trebuie sa fie egala
cu r0.
20) A doua conditie se scrie similar si deducem:
![]()
30) Din a treia conditie de optim deducem:
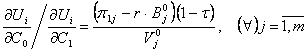
Cele 3 conditii definesc corelatiile fundamentale de echilibru intre cele 4 subsisteme:
- gospodariile, prin RMS intertemporala a consumului
- pietele financiare, prin r0, r, ![]()
- firmele prin ![]() si
si ![]()
- sistemul fiscal prin ![]() si
si ![]()
a) Din primele doua conditii deducem cerinta:
![]()
Fie ![]() rata de impozitare la
echilibru:
rata de impozitare la
echilibru: ![]()
Cum ![]() sunt fixate exogen
(prin legislatia fiscala) rezulta ca multimea gospodariilor se partitioneaza in
trei categorii:
sunt fixate exogen
(prin legislatia fiscala) rezulta ca multimea gospodariilor se partitioneaza in
trei categorii:
- platitori de
taxe mari - platitori de
taxe reduse - platitori de taxe medii

Corespunzator formulam criteriul de decizie optima de plasament:
i) Pentru categoria ![]() , randamentul efectiv corectat prin taxe al titlurilor
, randamentul efectiv corectat prin taxe al titlurilor ![]() este inferior
randamentului plasamentului in actiuni (neimpozabile):
este inferior
randamentului plasamentului in actiuni (neimpozabile):
![]()
Decizia lor va fi sa investeasca in actiuni.
ii) Pentru categoria ![]() , situatia este inversa:
, situatia este inversa:
![]()
Decizia lor este sa investeasca in obligatiuni.
iii) Pentru categoria ![]() , pentru care
, pentru care ![]() , decizia este indiferenta: exista substituibilitatea
perfecta intre cele doua categorii de plasamente.
, decizia este indiferenta: exista substituibilitatea
perfecta intre cele doua categorii de plasamente.
b) Din prima si a treia CNO se deduce:
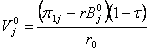
adica expresia care defineste valoarea
bursiera a firmei ![]() , in functie de factorii determinanti: firma (prin
, in functie de factorii determinanti: firma (prin ![]() si
si ![]() ), piata financiara (prin
), piata financiara (prin ![]() si
si ![]() ) si sistemul fiscal (prin
) si sistemul fiscal (prin ![]() ).
).
B. Decizia optima a
firmei privind finantarea prin imprumuturi ![]() este rezultatul
echilibrului cerere-oferta pe piata obligatiunilor (oferta lansata de firma,
este rezultatul
echilibrului cerere-oferta pe piata obligatiunilor (oferta lansata de firma, ![]() , cu cererea categoriei
, cu cererea categoriei ![]() de gospodarii).
Obtinem a patra conditie necesara de optim:
de gospodarii).
Obtinem a patra conditie necesara de optim: ![]() , adica:
, adica:
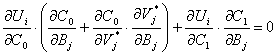
din care deducem:
40) 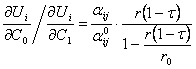
c) Din CNO (1) si (4) identificam decizia optima de plasament in actiuni la firma ![]() a gospodariei
a gospodariei ![]() .
.
![]()
Consecinta:
iv) daca ![]() deci va creste cererea
de actiuni fata de perioada de baza.
deci va creste cererea
de actiuni fata de perioada de baza.
v) daca ![]() situatia este inversa,
deci proprietarii (actionarii) vor vinde din actiunile detinute deja reducand
cota lor
situatia este inversa,
deci proprietarii (actionarii) vor vinde din actiunile detinute deja reducand
cota lor ![]() pana cand piata
bursiera reflecta echilibrul optim
pana cand piata
bursiera reflecta echilibrul optim ![]() .
.
Comparand conditionarile echilibrului optim ![]() cu
cu ![]() se deduce ca nivelul
optim al ratei medii de impozitare a gospodariilor este
se deduce ca nivelul
optim al ratei medii de impozitare a gospodariilor este ![]() (acelasi nivel cu cel
al firmelor); asadar pragul
(acelasi nivel cu cel
al firmelor); asadar pragul ![]() dupa care gospodariile
se structureaza in categoriile
dupa care gospodariile
se structureaza in categoriile ![]() de platitori de
impozite, care iau deciziile corespunzatoare de plasament i, ii, iii), este
chiar rata de impozitare a firmelor.
de platitori de
impozite, care iau deciziile corespunzatoare de plasament i, ii, iii), este
chiar rata de impozitare a firmelor.
Studii de caz Reformulati modelul Miller
pentru un sistem cu n = 3, m_= 2 (trei
gospodarii reprezentative, doua firme), prima gospodarie fiind de tip ![]() , a 2-a din categoria
, a 2-a din categoria ![]() si a treia din
categoria
si a treia din
categoria ![]() . Deduceti concret deciziile optime de plasament.
. Deduceti concret deciziile optime de plasament.
In conditiile actuale, la noi, trebuie folosit indicatorul definit prin (14), intrucat rδ nu este neglijabil: pentru r=50%, δ=8%, rezulta rδ=4%
Nota:
Indicatorii, proprietatile lor pentru aceste functii, tipologia lor si a
progresului tehnic, precum si modalitatile practice de identificare sunt
prezentate in capitolul I,
§ 1.5.1
|
Politica de confidentialitate
|
Despre managementul productiei |
||||||||||
Stiu si altele ... |
||||||||||
|
||||||||||