Utilizarea graficelor in analiza economica

UTILIZAREA GRAFICELOR IN ANALIZA ECONOMICA

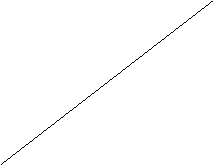
Microeconomia si macroeconomia folosesc in mod frecvent analiza grafica. Aceasta constituie un instrument extrem de util pentru intelegerea relatiilor economice si desprinderea concluziilor necesare.

Graficul, instrument de analiza economica

Graficele utilizate in aceasta carte sunt bidimensionale exprimand relatia functionala existenta intre doua variabile. Relatia functionala dintre doua variabile presupune ca valoarea unei variabile sa se modifice la cresterea sau scaderea unei alte variabile. In acest caz, se spune ca prima variabila depinde sau este functie de cea de a doua. Este posibila insa si folosirea unei a treia variabile, caz in care se studiaza influenta modificarii valorii ei asupra primelor doua variabile.

Intre doua variabile poate exista fie o relatie de directa proportionalitate, fie o relatie de inversa proportionalitate. In primul caz, ambele variabile evolueaza in acelasi sens, respectiv cresterea uneia este insotita de cresterea celeilalte. Si invers, reducerea unei variabile determina scaderea celeilalte variabile. De exemplu, relatia existenta intre pretul unitar si cantitatea oferita dintr-un produs este direct proportionala. In schimb, relatia dintre pretul unitar si cantitatea ceruta este invers proportionala.

Presupunem ca s-a putut determina o relatie functionala liniara intre cantitatea vanduta dintr-un bun si incasarile unui producator. Cantitatea vanduta este reprezentata pe axa OX ia 434b14e r incasarile producatorului pe axa OY. Datele se pot trece intr-un tabel (tabelul 2.1) si reprezenta grafic (figura 2.1)[1]. Pentru simplificare s-au considerat doar patru niveluri ale cantitatii vandute. Se poate constata ca fiecarui nivel dat de cantitate ii corespunde un anumit nivel al incasarilor.

Un exemplu de relatie directa intre doua variabile

Tabelul 2.1

Y

8 A₄

6 A₃

4 A₂

2 A₁

0 1 2 3 4 X

Fig. 2.1 Graficul relatiei direct proportionale intre doua variabile

In alte situatii, intre variabilele X si Y poate exista o relatie invers proportionala, caz in care cresterea unei variabile este insotita de reducerea celeilalte variabile. Cresterea pretului determina reducerea cantitatii cerute, dupa cum reducerea pretului stimuleaza cresterea cantitatii cerute. Datele sunt sintetizate in tabelul de mai jos si reprezentate in figura 2.2.

Un exemplu de relatie invers proportionala intre doua variabile

Tabelul 2.1

Y

B₁

3 B₂

B₃

B₄

0 1 2 3 4 X

Fig. 2.2 Graficul relatiei invers proportionale intre doua variabile

In fiecare dintre graficele anterioare s-a reprezentat o singura dreapta, deci o singura relatie functionala intre variabile. Adesea, este util a avea in acelasi sistem de coordonate doua sau mai multe drepte (sau curbe). Diagrama obtinuta este, in consecinta, multicurba, reprezentand concomitent mai multe relatii functionale. De exemplu, graficul cererii si ofertei, este util pentru determinarea pretului si cantitatii de echilibru precum si pentru furnizarea altor concluzii importante.

In legatura cu variabilele utilizate este important de precizat ca ele pot fi variabile discrete sau variabile continue. Variabilele discrete sunt cele care nu pot fi divizate in unitati infinitesimale, in timp ce pentru cele continue este posibila reprezentarea lor in fractiuni oricat de mici. De exemplu, in cazul unui producator de echipamente industriale, calculul cifrei de afaceri se realizeaza pentru cantitati exprimate in numere intregi si nu in fractiuni de echipamente. Pentru un fermier, acelasi calcul permite utilizarea variabilei cantitate de grau vanduta fractionata in unitati chiar infinitesimale.

Economistii fac adesea abstractie de tipul variabilei, discreta sau continua, interesul lor fiind mai degraba acela de a evidentia tipul de relatie functionala posibila intre variabilele economice.

Conceptul de panta si utilizarea sa in analiza economica

Conceptul de panta este foarte util in analiza economica, permitand desprinderea unor concluzii importante privind comportamentul economic si relatiile dintre diferite variabile economice.

Panta unei curbe masoara rata cu care variabila Y se modifica atunci cand X variaza. Altfel spus, panta este data de raportul DY/DX, termenii DY si DX semnificand cresterea sau scaderea fiecarei variabile.

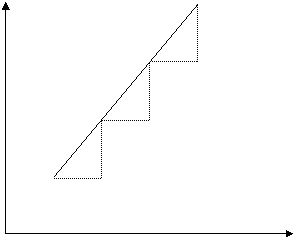
Consideram o relatie functionala intre doua variabile economice intre care exista o relatie direct proportionala (figura 2.3). Se observa ca fiecarei unitati suplimentare din variabila X ii corespunde o crestere cu 1,5 unitati din variabila Y. In consecinta, panta dreptei este DY/DX = 1,5/1 = 1,5.

Y

6 D

DY = 1,5

4,5 C

DX = 1

DY = 1,5

3 B DX = 1

DY = 1,5

1,5 A

DX = 1

0 1 2 3 4 X

Fig. 2.3 Panta unei drepte in conditiile unei relatii direct

proportionale intre variabile

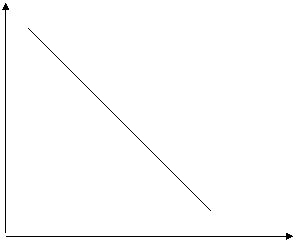
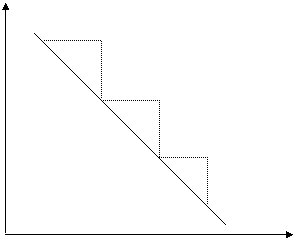
O dreapta orientata in jos are panta negativa. Cresterea variabilei X este insotita de scaderea variabilei Y (figura 2.4). Cum DY este de fiecare data -2 cand DX = 1, rrezulta ca panta dreptei este -2/1 = -2.

Y

DX = 1

8 A

DY = -2

DX = 1

6 B

DY = -2

4 DX = 1

C

DY = -2

2

D

0 1 2 3 4 X

Fig. 2.4 Panta unei drepte in conditiile unei relatii inverse

intre variabile

In situatia in care relatia functionala apare sub forma unei linii drepte (precum in cazurile anterioare) panta este constanta in orice punct al dreptei.

Cunoasterea pantei unei drepte indica relatia existenta intre variabila X si variabila Y. Astfel, panta poate fi:

a)    un numar pozitiv, caz in care cele doua variabile se modifica in acelasi sens (ambele cresc sau ambele descresc);

b)   un numar negativ, caz in care cele doua variabile evolueaza in directii opuse;

c)    zero, caz in care orice modificare a variabilei X nu genereaza nici-o modificare a variabilei Y. Dreapta exprimand relatia dintre cele doua variabile este paralela cu axa OX.

Modificarea pantei de-a lungul unei curbe

In exemplele anterioare s-a presupus existenta unei relatii de tip liniar intre variabile. Exista insa frecvente cazuri cand aceste relatii directe sau inverse sunt reprezentate printr-o curba (relatia devine curbilinie). De aceasta data, panta nu mai este aceeasi, ci se modifica de-a lungul curbei. Pentru a afla panta unei curbe intr-un punct se calculeaza tangenta in acel punct.

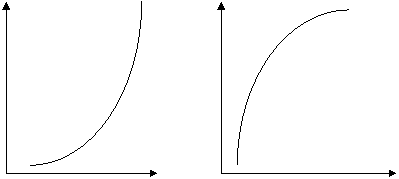
In situatia unei relatii direct proportionale intre cele doua variabile, curbele pot fi, dupa caz, convexe sau concave (figura 2.5 a si 2.5 b).

Y Y

0 X 0 X

a) b)

Fig. 2.5 Curbe convexe si concave in cazul relatiei direct

proportionale intre variabile

In figura 2.5 a, panta curbei creste pe masura ce valoarea variabilei X creste, ceea ce inseamna ca fiecare unitate suplimentara din X este insotita de o crestere tot mai mare a variabilei Y. Curba este in acest caz convexa. In schimb, in cazul figurii 2.5 b panta curbei descreste, iar curba este concava.

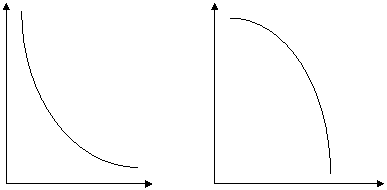
Daca relatia dintre variabila X si variabila Y este invers proportionala, cresterii variabilei X ii corespunde scaderea variabilei Y, insa cu rate diferite, in functie de forma curbei.

In cazul unei curbe convexe inspre origine, panta este negativa si in scadere (figura 2.6 a). In schimb, pentru o curba concava inspre origine, panta este tot negativa insa inregistreaza tendinta de crestere (figura 2.6 b).

Y Y

0 X 0 X

a)                             b)

Fig. 2.6 Curbe convexe si concave in cazul relatiei invers proportionale intre variabile

Panta si valorile extreme ale variabilelor

In analiza economica se intalnesc adesea situatii cand una si aceeasi curba poate prezenta toate cele trei tipuri de pante - pozitiva, negativa si zero. De exemplu, curba din figura 2.7 are mai intai o panta pozitiva si apoi negativa, trecand printr-un punct de maxim notat cu E, unde panta curbei este zero. Coordonatele acestui punct E dau valoarea lui X pentru care Y are valoare maxima.

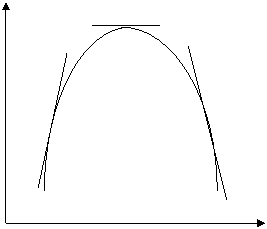
Y Panta zero

E

Panta Panta

pozitiva negativa

B C

A D

X

Fig. 2.7 Forma curbei la trecerea de la relatia direct

proportionala la relatia invers proportionala

Tot atat de adevarat este ca o panta de nivel zero poate insemna si o valoare minima pentru Y, situatie in care panta este mai intai negativa si apoi pozitiva (figura 2.8). Coordonatele punctului F dau valoarea lui X pentru care Y are valoare minima.

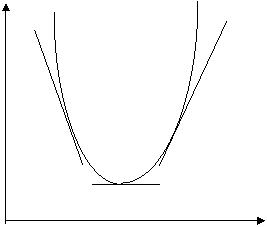
Y A D

Panta Panta

negativa pozitiva

B C

F

0 X

Fig. 2.8 Forma curbei la trecerea de la relatia invers

proportionala la relatia direct proportionala

Un caz interesant de curba care isi modifica concavitatea (si panta) odata cu trecerea de la relatia directa la una inversa este cea a ofertei individuale de munca (figura 2.9).

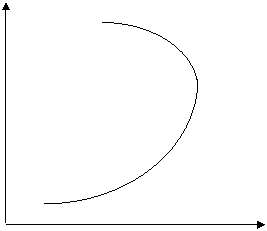Salariul

orar

(lei)

Curba ofertei

individuale de munca

0 Cantitatea de

munca oferita (ore)

Fig. 2.9 Oferta individuala de munca

Cresterea salariului determina angajatul sa lucreze mai multe ore, cel putin pana la un punct. Obtinerea unui salariu considerat corespunzator si cresterea lui in continuare schimba preferintele individuale in favoarea timpului liber. Se observa faptul ca graficul are un caracter abstract, nefiind insotit de date concrete. El nu vizeaza decat o relatie de ordin calitativ intre variabilele economice.

REZUMAT

Relatia functionala dintre doua variabile presupune ca valoarea unei variabile sa se modifice la cresterea sau scaderea unei alte variabile. In acest caz, se spune ca prima variabila depinde sau este functie de cea de a doua.

Intre doua variabile poate exista fie o relatie direct proportionala, fie o relatie invers proportionala. In primul caz, variabilele evolueaza in acelasi sens; ambele cresc sau ambele descresc. In cel de al doilea caz, variabilele evolueaza in directii opuse; cresterea unei variabile este insotita de descresterea celeilalte variabile.

Variabilele utilizate pot fi discrete sau continue. Variabilele discrete sunt cele care nu pot fi divizate in unitati infinitesimale, in timp ce pentru cele continue este posibila reprezentarea lor in fractiuni oricat de mici. Economistii fac adesea abstractie de tipul variabilei, discreta sau continua, interesul lor fiind mai degraba acela de a evidentia tipul de relatie functionala posibila intre variabilele economice.

Panta unei curbe masoara rata cu care variabila Y se modifica atunci cand X variaza. Panta este data de raportul DY/DX, termenii DY si DX semnificand cresterea sau scaderea fiecarei variabile.

Curbele exprimand o anumita relatie functionala intre variabile pot fi convexe sau concave. In cazul unei curbe convexe inspre origine, panta este negativa si in scadere In schimb, pentru o curba concava inspre origine, panta este tot negativa insa inregistreaza tendinta de crestere.

Ñ Termeni cheie

Relatie functionala Relatie direct proportionala Relatie invers proportionala Variabila discreta Variabila continua Panta Curba convexa Curba concava

Intrebari de verificare

1. Explicati natura relatiei dintre variabilele economice si, pe baza unui exemplu, reprezentati grafic fiecare situatie.

2. Trasati pe un grafic relatia posibila intre numarul de ore prestate de un angajat si salariul obtinut de acesta. Apreciati daca graficul se modifica in functie de abilitatea salariatului. Justificati raspunsul.

3. Intre numarul de ore de studiu si nota obtinuta la examen de catre studenti exista o relatie evidenta. Consideram ca acest numar este limitat la 10, iar nota probabila este cuprinsa intre 1 si 10. Trasati graficul corespunzator acestei relatii considerand alternativ numarul de ore de studiu reprezentat pe axa OX, iar apoi pe axa OY. Justificati forma graficului si puneti in evidenta semnificatia conceptului de panta.

4. Care este semnificatia unei linii orizontale ce intersecteaza axa OY ? Aceeasi intrebare in cazul unei linii verticale care intersecteaza axa OX.

5. Trasati graficul corespunzator relatiei intre doua variabile, in care panta este mai intai in scadere, iar apoi in crestere.

6. Completati tabelul urmator exprimand relatia existenta intre timpul liber si cel pentru studiu, astfel incat panta sa fie constanta. Numarul de ore afectat celor doua destinatii este 10. Precizati ce tip de relatie exista intre cele doua variabile si trasati graficul corespunzator.

Teste grila

1. Care dintre urmatoarele afirmatii nu constituie o relatie functionala intre variabilele X si Y?

a)    X creste iar Y ramane constant;

b)   cresterea lui X determina cresterea lui Y;

c)    reducerea lui X determina reducerea lui Y;

d)   reducerea lui X determina cresterea lui Y.

2. Care dintre urmatoarele afirmatii corespund conceptului de panta?

a)    variatia lui Y raportata la variatia lui X;

b)   modificarea in timp a variabilei X;

c)    modificarea in timp a variabilei Y;

d)   modificarea variabilei Y ce revine la modificarea cu o unitate a variabilei X;

e)    modificarea variabilei X ce revine la modificarea cu o unitate a variabilei Y.

3. O curba caracterizata mai intai printr-o relatie direct proportionala si panta in scadere, apoi printr-o relatie invers proportionala si panta in crestere trece:

a)    printr-un punct de maxim;

b)   printr-un punct de minim;

c)    nu se poate preciza daca punctul este de maxim sau de minim.

4. Unei relatii functionale invers proportionale ii corespunde o panta:

a)    negativa;

b)   pozitiva;

c)    pozitiva sau negativa, dupa caz;

d)   zero.