MANAGEMENT Termenul Management a fost definit de catre Mary Follet prin expresia "arta de a infaptui ceva impreuna cu alti oameni". Diferite informatii care te vor ajuta din domeniul managerial: Managementul Performantei, Functii ale managementului, in cariera, financiar.

StiuCum Home » MANAGEMENT » management general
Metode si modele utilizate in management
METODE SI MODELE UTILIZATE IN MANAGEMENT METODA PROGRAMARII LINIARE Utilizata in optimizarea proceselor: determinarea sortimentului optim de productie; repartizarea optima a resurselor. Problema de programare liniara cuprinde: variabile de decizie: x1, x2, . , xp; j = 1,p functia obiectiv: Z - expresia matematica ce masoara atingerea scopului optimizare: maximizarea sau minimizarea functiei obiectiv coeficientii functiei obiectiv: cj restrictiile problemei coeficientii restrictiilor conditie de nenegativitate modelul matematic: B. METODA DRUMULUI CRITIC - MDC (Critical Path Method - CPM) MDC - metoda euristica ce consta in identificarea activitatilor "critice" care influenteaza in mod hotarator durata totala a procesului. Definirea grafului - G G = (N, F) - graf de ordinul n N = (n1, n2, , nn) - multime finita; F - aplicatie multivoca definita pe aceasta multime. n1 n2 n4                n5 n3 nod izolat bucla Varfuri adiacente - varfuri legate printr-un arc Scopul grafului - modelarea matematica a unui proces complex, construit dintr-un ansamblu de activitati a caror succesiune logica alcatuieste un sistem organizat Particularitati: are un singur nod initial; are un singur nod final; nu admite circuite; nu admite noduri izolate. Drum critic - succesiunea in timp a activitatilor critice. Programarea si conducerea operativa a proceselor complexe se realizeaza in doua etape: elaborarea programului optimizat analiza structurii procesului complex constructia grafului calculul parametrilor grafului si stabilirea drumului critic analiza si optimizarea programului initial conducerea operativa a desfasurarii in timp a lucrarilor pe baza grafului stabilit Elaborarea programului optimizat o    Analiza structurii procesului complex Faza de conceptie bazata pe studiul documentatiei tehnice. stabileste lista activitatilor; stabileste succesiunea logica si interdependenta dintre activitatile procesului; precizeaza data inceperii si termenii lucrarii. Eveniment - moment semnificativ in desfasurarea procesului; nu consuma timp si resurse. Activitatea - actiune ce conduce la modificarea procesului; consuma timp si resurse. Caracteristicile activitatilor durata resursele consumate costul Reprezentarea activitatii si a evenimentelor A(dij) i                            j o       Constructia graficului retea Elementele graficului Noduri = evenimente Sageti = activitati A1 A2 1 2 3 4 5

 

Reguli de constructie a grafului

nu se construieste la scara;

urmareste respectarea succesiunii cronologice si a interdependentei tehnologice;

are un singur nod initial si unul singur final;

doua noduri nu pot fi legate prin doua sau mai multe arce;

nu se admit circuite, bucle.

o       Calcul parametrilor grafului si stabilirea drumului critic

T_f - termenul calendaristic final planificat

T_i - termenul calendaristic initial

t - termenele evenimentelor

termenul minim

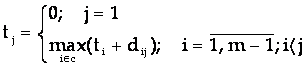
c - multimea nodurilor "i" din care pleaca arce convergente in nodul 'j'

t_m - termenul minim al evenimentului final

t_m < T_f ; t_m = T_f ; t_m > T_f

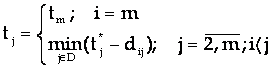termenul maxim

D - multimea nodului "j" catre care diverg arce ce pleaca din noduri "i"

M_i - marja de timp

M_i = t^*_i - t_i

M_i > 0 ; M_i = 0 ; M_i < 0

termenele activitatilor

t_ij - termenul cel mai devreme de inceput:

t^t_ij - termenul cel mai devreme de sfarsit:

t^*t_ij - termenul cel mai tarziu de sfarsit:

t^*i_ij - termenul cel mai tarziu de inceput:

rezervele de timp

R_tij - rezerva totala:

Rt_ij £ 0 - activitate critica

Rt_ij > 0 - exista rezerva de timp

R_tij - rezerva libera - numai pentru activitatea necritica

t_i = tⁱ_ij t^t_ij = t_j t^*_i = tⁱ_ij t^*_j = t^*t_ij

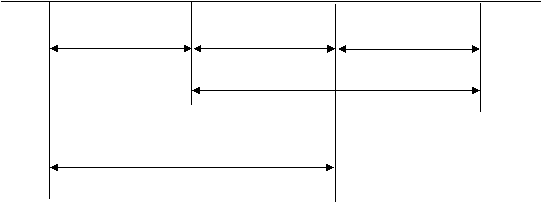
d_ij                         Re_ij d_ij

Rt_ij

Rl_ij

o       Analiza si optimizarea programului initial

C. METODA PERT - Program Evaluation and Review Technique

Metoda PERT abordeaza problema programarii si conducerii operative a unui proces din punct de vedere probabilistic.

se bazeaza pe aceleasi principii ca MDC

duratele activitatilor nu sunt valori certe ci variabile aleatoare caracterizate prin media si dispersia lor

Trasaturile metodei PERT

durata unei activitati este evaluata prin trei estimari: pesimista, probabila si optimista;

procesul este reprezentat printr-o retea in care accentul este pus pe evenimente;

se admite pentru usurinta calculelor legea "b" de distributie.

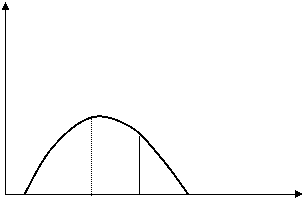p

a_ij m_ij t_ij b_ij durata

Legea de distributie de tip "b" a probabilitatilor de aparitie a

tuturor duratelor posibile ale unei activitati

Distributia "b" satisface conditiile:

intersecteaza axa absciselor in doua puncte a_ij si b_ij corespunzatoare duratei minime si maxime;

este unimodala, adica exista o singura valoarea maxima (m_ij) care reprezinta durata cea mai probabila sau modulul distributiei.

Elementele utilizate in metoda PERT:

a_ij - durata optimista - durata minima de executie a unei activitati;

m_ij - durata probabila - estimatia duratei cu cea mai mare sansa de realizare in conditiile normale de lucru;

b_ij - durata pesimista - intervalul de timp maxim de realizare a activitatii ij.

t_ij - durata medie a activitatii

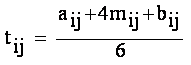
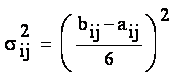
s _ij - dispersia activitatii

z - factor de probabilitate

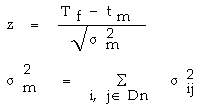
p (t_m £ T_f) - probabilitatea ca durata proiectului sa fie mai

mica sau cel mult egala cu T_f

p ( t_m £ T_f) < 0,25 - risc mare

p ( t_m £ T_f) = 0,5 - programare justa

p ( t_m £ T_f) > 0,5 - resurse utilizate excesiv

D. TEORIA DECIZIEI

Planificarea se realizeaza prin urmatoarele categorii de decizii:

identificarea obiectivului dorit;

folosirea metodelor de prognoza;

gasirea strategiei de atingere a obiectivului propus;

determinarea cantitativa si calitativa a resurselor.

Scopul luarii deciziei

implicarea managerilor de la orice nivel;

supravietuirea, dezvoltarea organizatiei.

Decizia reprezinta un mecanism dinamic, rational, prin care un manager, alegand o anumita varianta din mai multe posibile, urmareste atingerea unui anumit obiectiv.

Etapele procesului decizional

Elementele procesului decizional

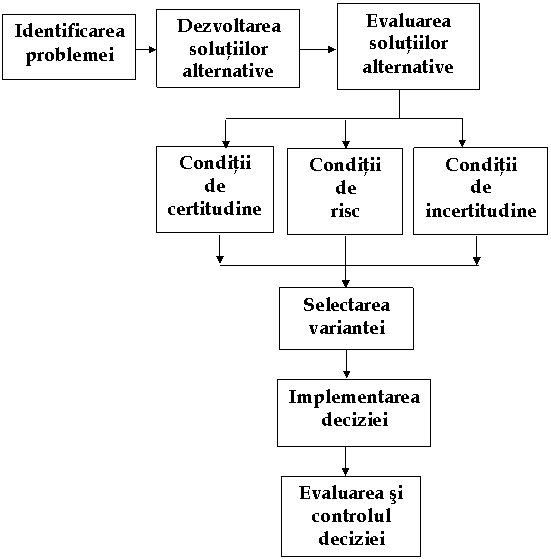
decidentul - individ sau grup

multimea variantelor - multimea modurilor de realizare a unei actiuni:

V = i = 1, m

multimea criteriilor de decizie reprezinta punctul de vedere care se ia in considerare atunci cand se alege cea mai buna varianta:

X = j = 1, n

multimea starilor naturii - suma conditiilor interne si externe ale firmei in care se aplica variantele decizionale:

N = k = 1, k

multimea consecintelor - reprezinta rezultatele fiecarui mod de actiune in conditiile definite:

C =

Clasificarea proceselor decizionale

o       functie de elementele ce intervin in proces:

dupa decident :

cu decident individual

cu decindentul colectiv

dupa numarul variantelor decizionale

cu numar finit de variante

cu numar infinit de variante

dupa multimea criteriilor de decizie:

unicriteriale

multicriteriale

dupa starile naturii in care se desfasoara procesul:

conditii de certitudine

conditii de risc

conditii de incertitudine

o       functie de nivelul managerial la care se desfasoara procesul decizional:

strategice

tactice

curente

Conceptul de utilitate

Utilitatea decizionala este gradul de satisfactie al decidentului in urma realizarii unei anumite consecinte a variantei alese.

o       Axiomele utilitatii:

Intre doua variante decizionale (V_i, V_j) poate exista numai una din urmatoarele relatii:

V_i P V_j; V_j P V_i; V_i I V_j

P - operator logic de preferinta

I - operator logic de indiferenta

Relatiile de preferinta sunt tranzitive:

fie trei variante decizonale (V_i, V_j, V_k)

daca V_i P V_j si V_j P V_k atunci V_i P V_k

Relatiile de indiferenta sunt tranzitive si reflexive sau simetrice:

daca V_i I V_j si V_j I V_k atunci V_i I V_k

V_i I V_j Û V_j I V_i

In afara multimii V = (V₁, V₂, ., V_n) a variantelor simple, decidentul poate lua in considerare si variante complexe:

V' = pV_i + (1-p)V_j

p - probabilitatea de realizare a variantei V_i

(1 -p) - probabilitatea de realizare a variantei V_j

Fie trei variante V_i, V_j , V_k pentru care se exprima realatia V_i P V_j P V_k Þ exista un mix

V' = p' V_i + (1-p' )V_k astfel incat V' P V_j si un alt mix

V" = p" V_i + (1-p" )V_k astfel incat V_j P V^"

Fie trei variante V_i, V_j , V_k pentru care se exprima relatia V_i P V_j atunci va exprima explicit relatia

pV_i + (1-p)V_k P pV_j + (1-p)V_k

Functia de utilitate are forma:

u : V R            V =

V_i P V_j                  u (V_i) P u (V_j)

V_i I V_j                   u (V_i) I u (V_j)

V_i P V_j P V_k          u pV_j, (1-p)V_k P u pV_j, (1-p)V_k

Etape de rezolvare

Se construieste matricea consecintelor

Se transfera matricea consecintelor in matricea utilitatilor

se aleg coeficientii de importanta ai criteriilor

se aloca utilitatile astfel:

c_fav u_max = k_j

c_def u_min = 1 - k_j unde k_j I

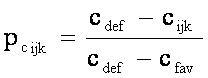
u(c_ijk) = pc_ijk . u_max + (1-p_ijk) . u_min

se determina varianta optima pentru diferite conditii:

certitudine:        

risc:                     

incertitudine:

- criteriul pesimist (Wald) :

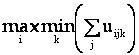
- criteriul optimist (Hurwitz) :   

- criteriul rezultatelor (Savage) :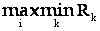

- criteriul optimismului ponderat (Laplace):