Studiul tehnologiei firmei, functii de productie

Notiuni introductive

Alaturi de consumator, firma reprezinta al doilea factor sau actor al procesului economic.

O firma reprezinta o entitate creata de oameni in vederea atingerii unor anumite obiective. Aceasta entitate va achizitiona inputuri (factori de productie) si ii va combina in vederea obtinerii productiei, a outputului.

Inputurile sunt achizitionate de pe pietele factorilor de productie si contravaloarea acestora reprezinta in mod uzual costurile firmei. Productia va fi vanduta pe pietele bunurilor si serviciilor, iar in schimbul acesteia firma va incasa contravaloarea acesteia - veniturile.

Cel mai important motiv care sta la baza deciziei de a infiinta si conduce o firma il reprezinta obtinerea de catre proprietarii firmei a unui profit cat mai mare, profit care in mod uzual este definit ca diferenta dintre veniturile obtinute in urma vanzarii bunurilor si serviciilor produse si cheltuielile efectuate pentru cumpararea inputurilor folosite in procesul de productie si cele tehnologic induse de realizarea produsului finit.

Totusi, maximizarea profitului nu constituie singurul motiv al functionarii firmei. Alte scopuri ar putea fi maximizarea cotei pe piata detinute, a prestigiului sau a vanzarilor.

Chiar si in aceste conditii ipoteza maximizarii profitului ramane cea mai credibila si mai robusta in vederea previzionarii comportamentului firmei.

Functii de productie

Productia este procesul transformarii inputurilor in outputuri. Cea mai importanta conditie ce trebuie indeplinita in cadrul acestui proces este aceea a fezabilitatii tehnologice, respectiv a capacitatii firmei de a produce un anumit bun sau serviciu pornind de la inputurile avute la dispozitie.

Astfel, firma are la dispozitie o multime de inputuri pe care o vom nota cu X (multimea inputurilor, a factorilor de productie). Un vector reprezinta o combinatie de - inputuri folosite in procesul de productie. Evident, fiecare input va fi exprimat ca fiind o cantitate nenegativa x ³

Prin intermediul acestor inputuri firma va produce bunul (sau bunurile) dorite si fezabile tehnologic. Multimea posibilitatilor de productie va fi notata prin Y, si y I Y, cu reprezentand un vector al outputurilor produse de firma, cu y ³ )

Tehnologia pe care o are la dispozitie firma va fi descrisa prin intermediul functiei de productie, care va indica modul in care se pot combina inputurile in vederea obtinerii outputului (sau outputurilor) considerate.

Astfel, vom considera functia de productie f ca fiind o corespondenta dintre multimea inputurilor si multimea outputurilor.

Astfel:

,

cu:

X - multimea inputurilor,

Y - multimea outputurilor,

Observatie

Daca (spatiul unidimensional) atunci functia de productie se numeste monooutput sau monoproduct, iar daca , atunci functia de productie este numita multioutput.

Proprietati ale functiilor de productie

Cadrul axiomatic

Pentru inceput vom analiza functiile de productie monooutput.

Fie , o functie de productie monooutput. Atunci aceasta are urmatoarele proprietati:

Ipoteza 1

Functia de productie f(x) este:

a) continua;

b) de doua ori diferentiabila ^[2]).

Continuitatea functiei de productie f indica faptul ca existenta unor modificari mici ale inputurilor va conduce la modificari mici ale outputului produs.

Diferentiabilitatea functiei f este impusa din ratiuni de simplificare a analizei.

Ipoteza 2

Functia de productie este strict crescatoare in raport cu fiecare argument:

Daca:

si iar

atunci

Aceasta proprietate arata ca orice crestere a unuia dintre inputuri (factori de productie) va conduce la cresterea outputului.

Ipoteza 3

Multimea factorilor de productie, X, este o multime nevida, compacta si convexa.

Ipoteza 3 este una simplificatoare care arata ca nu pot exista restrictii asupra factorilor de productie achizitionati de firma, deci aceasta se poate dota cu cantitatea dorita in orice moment. In realitate, aceasta ipoteza este infirmata deseori in practica, dar pentru zonele pe care le vom analiza, ipoteza este adevarata.

Ipoteza 4

Functia de productie este concava (cvasi-concava) pe multimea , sau:

pentru orice .

Ipoteza de concavitate arata faptul ca orice combinatie convexa de inputuri (respectiv alegerea, din doi vectori diferiti de inputuri, a unui al treilea format din anumite proportii ale primelor doua) va conduce la un output care va fi mai mare decat outputul format din aceleasi proportii ale outputurilor determinate de factorii de productie (inputurile) initiali si .

O alta interpretare a proprietatii ale cvasi-concavitate este aceea data de alegerea randamentelor marginale descrescatoare, care afirma faptul ca orice crestere a inputurilor va conduce la cresterea outputurilor, dar cu o proportie mai mica decat majorarea inputurilor.

Observatie

Daca f este de clasa C₁ atunci f '(x) > 0 ( ) x I X.

Ipoteza 5

a) ,  

b) .

Aceasta ipoteza indica faptul ca daca nu exista inputuri (sau cel putin unul dintre ele) atunci productia nu poate fi realizata (outputul este nul).

Ipoteza 6

Functia de productie este finita

Ipoteza 6 ne arata faptul ca pentru un vector al inputurilor (resurselor, factorilor de productie) dat, productia ce poate fi obtinuta pe baza acestuia este finita (respectiv exista un output maxim ce poate fi obtinut cu un input dat).

Exemple

Exemplul 1.1. Functia de productie Leontief

,

cu parametri pozitivi,,

Daca (exista doar doua inputuri) atunci in figura 1.1 este reprezentata aceasta functie de productie de tip Leontief: .

Observatie

Frontierele de productie ale multimii sunt date de daca valoarea functiei este si daca este data de . Aceasta functie respecta ipotezele prezentate anterior. Daca x₁ = 0 Þ f = 0.

Exemplul 1.2.

Functia de productie Cobb-Douglas generalizata

Functia de productie Cobb-Douglas respecta toate ipotezele anterioare.

Exemplul 1.3.

Functia de productie C.E.S. (Constant Elasticity of Substitution)

Acest tip de functie de productie nu respecta ipoteza 5 b) (deoarece daca unul dintre inputuri este nul, 454i87e sau chiar toti) atunci functia de productie nu este nula (nu este definita pentru ).

Izocuante

Pentru un nivel fixat al productiei, , multimea inputurilor ce pot conduce la obtinerea acestui output se numeste izocuanta (sau y-izocuanta). Vom nota aceasta multime prin , si are urmatoarea expresie:

Pentru o functie de productie Cobb-Douglas cu doua inputuri si parametrii subunitari , in figura 1.2 sunt reprezentate diverse y-izocuante.

Nota: Izocuanta este locul geometric al factorilor care verifica f(x) = y. Astfel, pentru exemplul din figura 1.2, ecuatia izocuantei este:

x = = (C - constanta),

adica o hiperbola: cand x₁ Þ x₂ 0; cand x₁ ¥ Þ x₂ ¥, deci avand asimptotele: verticala x₁ = 0 si orizontala x₂ = 0.

Tema Determinati ecuatia izocuantei pentru functia cu
2 factori si trasati izocuantele y₁, y₂, y₃, .

Rate marginale de substitutie tehnica (RMST)

Rata marginala de substitutie tehnica (RMST) arata care sunt proportiile in care pot fi inlocuite inputurile intre ele astfel incat sa se obtina acelasi nivel al outputului.

Astfel, daca vom considera inputurile si , atunci rata marginala de substitutie tehnica intre inputurile si va fi notata cu:

Valoarea indicata de , in valoare absoluta, arata cate unitati din inputul i pot inlocui o unitate din inputul j astfel incat productia sa ramana la acelasi nivel.

Geometric, pentru o functie de productie cu doua inputuri, reprezinta panta tangentei la y-izocuanta intr-un punct fixat . (vezi figura 1.3).

Functii de productie separabile

Fie multimea tuturor inputurilor, iar aceasta multime o vom imparti in submultimi, in raport cu tipul de inputuri (de exemplu intr-o categorie de inputuri pot intra cele legate de forta de munca si utilizarea acesteia, in alta categorie intre inputurile ce contin materiile prime (exclusiv energia, sau o alta categorie ar putea fi cea a bunurilor de capital).

Definitia 1.1

Functia de productie este slab separabila daca rata marginala de substitutie tehnica dintre doua inputuri din aceeasi multime de inputuri este independenta de inputurile din alte grupe:

si

Functia de productie se numeste puternic separabila daca rata marginala de substitutie tehnica dintre doua inputuri din grupuri diferite este independenta de orice input care apartine acelor grupuri:

si

O concluzie ce deriva din separabilitatea factorilor de productie (a inputurilor) pe grupe este aceea ca procesul de productie al unei firme poate fi impartit pe stadii de productie, in fiecare stadiu utilizandu-se doar anumite inputuri si obtinandu-se outputuri (posibil) intermediare.

Astfel, daca prin vom nota functiile de productie pe stadii (pe etape) de fabricatie, atunci separabilitatea slaba a functiei de productie permite scrierea acesteia ca fiind:

cu strict crescatoare si qvasi-concava iar - functii de productie partiale ce satisfac toate proprietatile necesare.

In prima etapa a agregarii vor fi folositi factorii pentru producerea inputurilor intermediare , pentru ca in cea de-a doua etapa sa se obtina outputul final pe baza functiei de productie .

Observatie

Daca o functie de productie este separabila tare, atunci ea este si slab separabila.

Exemplul 1.4.

Functia de productie Cobb-Douglas este separabila in factori

Fie(daca vom defini functia Cobb-Douglas in termen de inputuri agregate). Atunci productivitatea marginala a unui input dintr-o clasa va fi:

De aici rezulta ca norma diferentiala de substituire intre si este:

Acest termen depinde doar de si de , prin urmare derivata in raport cu oricare alt input din alta grupa este nula. Deci, functia de productie Cobb-Douglas este separabila.

Indicatorii functiilor de productie

Pentru a se putea utiliza si analiza corespunzator activitatea unei firme (ce este descrisa prin intermediul unei functii de productie) vom determina indicatorii specifici asociati.

Astfel vom avea cinci categorii de indicatori.

Tipologia si calculul indicatorilor

a) indicatori medii

Data fiind functia de productie , indicatorii medii arata modul in care se obtine outputul pe baza fiecarui input, sau cu cat poate fi modificat in medie outputul prin modificarea unui anumit input cu o unitate:

unde:

- productivitatea medie a inputului ;

- outputul obtinut

- cantitatea din inputul utilizata pentru producerea outputului .

b) indicatori marginali

Indicatorii marginali vor arata modul in care se modifica outputul in raport cu modificarile marginale ale inputurilor, sau cu alte cuvinte, cu cate unitati se va modifica outputul daca vom creste cu o unitate, fata de nivelul dat, un anumit input:

unde:

- reprezinta productivitatea marginala a inputului ;

- derivata partiala a functiei de productie in raport cu factorul ;

c) indicatori procentuali (elasticitati)

Indicatorii procentuali (sau elasticitatile) vor arata modificarile procentuale ale outputului in raport cu modificarile procentuale ale inputurilor, sau altfel spus, cu cate procente se va modifica outputul la modificarea cu un procent a unui anumit input:

sau:

Elasticitatea factorilor mai poate fi determinata ca raport intre productivitatea marginala si productivitatea medie a factorului considerat.

d) Rate marginale tehnice de substitutie (RMST)

O rata marginala de substitutie va arata care este cantitatea necesara dintr-un anumit input ce poate fi utilizata pentru a inlocui o unitate din alt input astfel incat productia obtinuta sa ramana la acelasi nivel. Astfel, de-a lungul izocuantei y = f (x), y - fixat, diferentiind, obtinem:

Considerand numai modificarile a doi factori, respectiv i si j, cu dx_i ≠ 0, dx_j ≠ 0, si respectiv dx_k = 0 pentru orice k ≠ i,j, obtinem:

-

Rata marginala de substitutie tehnica mai poate fi determinata ca raport intre productivitatile marginale ale factorilor.

e) coeficientul elasticitatii ratei marginale de substituire (sau elasticitatea substituirii) este inversul elasticitatii RMST:

, unde elasticitatea RMST se calculeaza in raport cu nivelul relativ x_i /x_j de consum al celor doi factori, adica:

Deci, coeficientul elasticitatii RMST va fi:

Acest indicator arata cat de usor pot fi inlocuit un input cu un alt input.

Astfel, pentru functiile de productie qvasi-concave, este pozitiv . Cu cat valoarea acestuia se apropie de zero cu atat inputurile pot fi substituite mai greu (iar la limita, daca , atunci inputurile i si j nu pot fi substituite), iar daca este mare, atunci poate fi realizata o substituire "usoara" a inputurilor.

In figura 1.4 sunt reprezentate trei situatii posibile. Astfel in figura 1.4 a) izocuanta functiei de productie este liniara si atunci , adica avem o substituibilitate perfecta intre inputuri. In figura 1.4 c) , adica cele doua inputuri nu pot fi substituite, pentru ca in figura 1.4 b) sa avem o elasticitate a substituirii intermediara , deci sa poata efectua substituirea doar in anumite proportii:

Exemple

Exemplul 1.5.

Se considera functie de productie de tip Cobb-Douglas cu doi factori de productie, respectiv capitalul, , si forta de munca, .

Pentru functia de productie vom determina indicatorii asociati:

a) indicatorii medii:

- productivitatea (sau eficienta) medie a capitalului:

- productivitatea (eficienta) medie a muncii:

unde:

- , productivitatea medie a capitalului, arata cate unitati de productie se produc, in medie, prin intermediul unei unitati de capital

- , productivitatea medie a muncii, arata cate unitati de productie se obtin, in medie, prin intermediul unei unitati de forta de munca

Observatie   

Daca vom nota prin (inzestrarea tehnica a muncii, respectiv cate unitati de capital revin la o unitate de forta de munca) si , atunci obtinem urmatoarele relatii:

b) indicatorii marginali:

- productivitatea (eficienta) marginala a capitalului:

- productivitatea (eficienta) marginala a muncii:

Observatie   

In raport cu inzestrarea tehnica a muncii, , si pentru obtinem:

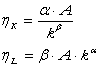
- productivitatea marginala a capitalului, , arata cu cate unitati poate fi majorata productia in conditiile in care nivelul capitalului va fi majorat cu o unitate fata de nivelul existent;

- productivitatea marginala a muncii, , arata cu cate unitati poate fi marita productia in conditiile in care nivelul muncii este marit cu o unitate fata de nivelul existent.

c) indicatorii procentuali (elasticitatile):

- elasticitatea capitalului, , arata cu cate procente se va modifica nivelul productiei daca nivelul capitalului se modifica cu un procent (de crestere sau scadere);

- elasticitatea fortei de munca, , arata cu cate procente se va modifica nivelul productiei daca nivelul fortei de munca utilizat se modifica cu un procent (crestere sau scadere).

d) rata marginala tehnica de substitutie:

Daca si in raport cu inzestrarea tehnica a muncii obtinem:

- rata marginala tehnica de substitutie indica, in acest caz, cate unitati de capital pot inlocui o unitate de forta de munca astfel incat productia sa ramana constanta.

Observatie

Rata marginala tehnica de substitutie se poate calcula si invers, respectiv prin a determina cate unitati de forta de munca pot inlocui o unitate de capital, pastrand nemodificat nivelul productiei:

e) coeficientul elasticitatii ratei marginale de substitutie (elasticitatea substitutiei)

Observatie: Tragem concluzia ca pentru orice functie Cobb-Douglas si, in particular, pentru o functie de productie de tip Cobb-Douglas in care (randamente constante la scala), elasticitatea ratei marginale de substitutie este intotdeauna unitara (1).

Exemplul 1.6

Consideram functia de productie de tip C.E.S. (Constant Elasticity of Substitution) exprimate in raport cu doi factori de productie (sa presupunem tot capital si munca, respectiv ) pentru simplificarea calculelor reluam cazul din exemplul 1.3, cu a_i = 1 si in loc de -r luam r

, cu

indicatorii medii:

indicatorii marginali:

indicatorii procentuali (elasticitatile):

rata marginala de substitutie tehnica:

e) elasticitatea ratei marginale de substitutie:

Observatie   

Denumirea functiei (C.E.S. - Constant Elasticity of Substitution) provine din faptul ca este constant, respectiv are valoarea . Propunem ca studiu de caz determinarea indicatorilor functiei CES cu doi factori in cazul general:

Y = A

Proprietati speciale

LEMA SHEPARD (pentru functii de productie)

Functiile de productie liniar omogene (omogene de gradul I) sunt concave.

Fie o functie de productie, , continua, strict crescatoare si strict cvasiconcava pe , iar si omogena de gradul 1. Atunci este o functie concava in .

Demonstratie.

Fie si .

Atunci (deoarece si f este strict crescatoare).

Cum este omogena de grad 1 (adica ):

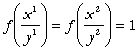
Cum este (strict) cvasiconcava, avem:

Alegem un (si

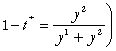
Atunci din rezulta:

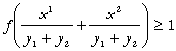
Din omogenitatea liniara a lui si din rezulta ca:

Relatia este adevarata pentru orice si . Dar, din conti­nuitatea functiei , rezulta ca este adevarata pentru orice si .

Pentru a completa demonstratia, vom considera si , si . Vom avea:

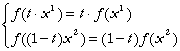(din omogenitatea liniara a functiei )

De aici, conform rezulta ca:

q.e.d.

Observatie

Interpretarea Lemei Shepard este urmatoarea: productia (optimala) a unei firme ce utilizeaza cantitatea de factori de productie este mai mare (cel mult egala) cu suma productiilor ce sunt realizate de doua firme ce utilizeaza cantitatile , respectiv de inputuri.

Astfel spus, agregarea inputurilor conduce la un output mai mare decat din utilizarea unor inputuri de acelasi nivel dar pe parti componente.

Randamentele la scala ale functiilor de productie

In multe analize timpul este unul din factorii esentiali. Astfel, atat analizele microeconomice cat si cele macroeconomice considera timpul la doua nivele distincte: pe termen scurt (short run) si respectiv pe termen lung (long run).

Analizele pe termen scurt presupun (in termenii teoriei producatorului) ca cel putin unul dintre inputuri este fixat in acea perioada, iar outputul poate fi modificat doar prin variatia celorlalte inputuri.

Pe termen lung firma isi poate varia toate inputurile.

Randamentul la scala al unei firme (pe o anumita perioada) va arata modul in care variaza outputul ca raspuns la variatia inputurilor.

Astfel, pe termen scurt vor varia doar inputurile nefixate, iar rezultatul variatiei acestora se va concretiza in variatia outputului.

Pe termen lung se vor varia toate inputurile cu aceeasi proportie si de aici va rezulta variatia outputului.

In raport cu aceasta variatie a outputului exista trei tipuri de functii de productie, respectiv cele cu randamente descrescatoare la scala, cu randamente constante la scala si cu randamente crescatoare la scala.

De asemenea, analizele pot fi efectuate atat la nivel global (pentru intreg domeniul de definitie), cat si local, in anumite puncte). Astfel, vom avea:

Definitia 1.2. Randamente globale la scala:

O functie de productie poate avea urmatoarele tipuri de randamente (globale):

- randamente constante la scala daca si ;

- randamente crescatoare la scala daca si ;

- randamente descrescatoare la scala daca si .

Observatii

1. O functie de productie va avea randamente constante la scala doar daca este o functie omogena de grad I.

2. Alte interpretari ale tipurilor de randamente la scala sunt urmatoarele:

a) pentru o functie cu randamente constante la scala o crestere cu un procent a tuturor inputurilor va conduce la cresterea tot cu un procent a outputurilor.

b) in cazul unei functii cu randamente crescatoare la scala, cresterea cu un procent a inputurilor va conduce la o crestere mai mare de un procent a outputului

c) pentru functiile cu randamente descrescatoare la scala, cresterea cu un procent a inputurilor va conduce la cresterea outputului dar cu mai putin de un procent a outputului.

Multe dintre functiile de productie ce satisfac Ipoteza 4 (de cvasiconcavitate) nu pot fi separate in cele trei categorii descrise anterior deoarece au comportamente diferite (constante, crescatoare sau descrescatoare) in raport cu nivele diferite ale outputurilor. Astfel, pentru a putea descrie aceste functii avem nevoie de o masura locala a randamentelor la scala.

Aceasta masura se mai numeste si elasticitatea scalei sau elasticitatea generala a outputului:

Definitia 1.3. Randamente locale la scala:

Elasticitatea scalei de fabricatie in punctul este:

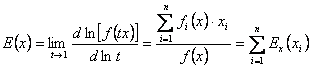
Astfel:

a) daca atunci functia de productie are randamente (locale) constante la scala;

b) daca atunci avem randamente crescatoare la scala;

c) daca atunci avem randamente descrescatoare la scala.

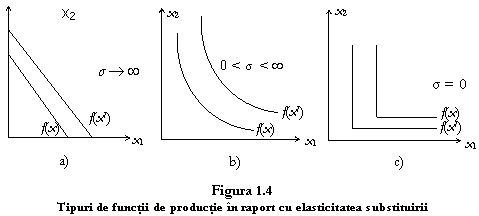
Astfel, functia de productie reprezentata in figura 1.5 are toate cele trei tipuri de randamente la scala:

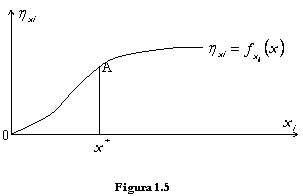
Astfel, daca atunci functia de productie are randamente crescatoare la scala, daca atunci avem randamente constante (local) la scala iar daca atunci functia de productie are randamente descrescatoare la scala.

Exemple

Exemplul 1.7. Fie functia de productie de tip Cobb-Douglas:

Pentru functia Cobb-Douglas am vazut ca elasticitatile sunt , respectiv:

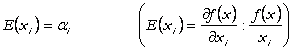
deoarece .

Astfel, din punct de vedere local vom avea urmatoarele tipuri de randamente la scala:

a) Daca randamente constante la scala.

b) Daca randamente crescatoare la scala.

c) Daca randamente descrescatoare la scala.

Pentru functia Cobb-Douglas randamentele globale si cele locale coincid.

Astfel:

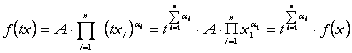
Deci, daca avem randamente globale constante la scala, iar daca avem randamente crescatoare la scala, respectiv daca rezulta randamente descrescatoare la scala.

Exemplul 1.8

Functia C.E.S. are randamente globale constante la scala:

Exemplul 1.9

Fie functia de productie:

, cu ,

iar nivelul superior al outputului ce poate fi obtinut, adica .

Vom determina nivelul local al randamentelor la scala pentru functia de productie data:  

Elasticitatile celor doua inputuri sunt:

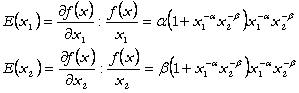
De aici:

care variaza in raport cu , deci vom avea randamente la scala diferite in raport cu nivelul inputurilor (deci si al outputului). Observam ca , si daca notam

deci:

De aici:

Este evident ca atat in raport cu fiecare input, cat si pentru intreaga functie de productie, randamentele la scala descresc pe masura ce inputul creste.

Pentru

Pentru

Daca atunci avem: randamente crescatoare la scala pentru .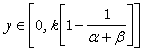

- randamente constante la scala pentru

- randamente descrescatoare la scala pentru .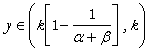

Legea proportiilor variabile

Legea proportiilor variabile este in esenta o reglementare a legii productivitatii marginale descrescatoare, dar pentru un caz mai general. Interpretarea acesteia este urmatoarea: daca vom creste succesiv un input (cu cantitati constante), pastrand celelalte inputuri fixate, atunci in prima faza vom inregistra o crestere a productiei mai mare decat cresterea inputului, iar dupa aceea cresterile outputului vor fi mai mici decat cresterea inputului.

Legea proportiilor variabile.

Fie o functie de productie. Atunci pentru fiecare input exista un nivel astfel incat:

a) daca atunci

b) daca atunci

c) daca atunci

In figura 1.6 este reprezentata grafic o asemenea functie de productie:

Productivitatea medie reprezinta panta razei ce uneste originea cu punctul . Productivitatea medie este maxima atunci cand este egala cu productivitatea marginala, (raza este tangenta la curba f (x_i)).

Conditia de maxim pentru productivitatea medie este:

(productivitatea medie este egala cu productivitatea marginala - punctul B din figura 1.6 ).

Pana in punctul A avem o productivitate marginala crescatoare in raport cu (avem ), iar dupa punctul A avem o productivitate marginala descrescatoare .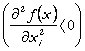

Unii economisti denumesc zona de utilizare a inputurilor dintre 0 si B - "primul stadiu al productiei", iar zona care urmeaza "al doilea stadiu al productiei". Punctul B mai este denumit "marginea extensiva" a productiei.

Masurarea gradului de substituire a factorilor

Proprietatea de substitutie a factorilor este fundamentala in analiza neoclasica dar nu poate fi considerata o lege economica. Exista si functii de productie cu factori complementari, in care outputul nu poate fi obtinut decat daca exista toate inputurile (functia de productie Leontief). Totusi, pentru functiile de productie neoclasice, gradul in care inputurile pot fi substituite este un indicator important pentru decidenti.

Definitia 1.4.

Vom numi input limitativ acel input a carui crestere reprezinta o conditie necesara (dar nu si suficienta) pentru ca outputul sa creasca.

In termenii descrisi de functia Leontief:

toti factorii pot fi considerati limitativi.

Fie multimea care descrie limita inferioara a outputului. Daca functia de productie este strict monotona si derivatele partiale de ordinul i nu se anuleaza atunci se pot rezolva ecuatia si sa se obtina solutia .

de aici rezulta ea.

(1)

Pentru a determina modificarea inputului in raport cu modificarea inputului (daca outputul si celelalte inputuri raman nemodificate) atunci vom deriva in raport cu , si vom obtine:

De aici rezulta ca:

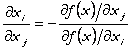
care reprezinta tocmai rata marginala de substitutie tehnica.

Elasticitatea ratei marginale de substitutie tehnica (directa) a fost introdusa pentru prima data de Hicks (1963).

Aceasta este:

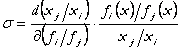
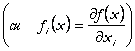
In figura 1.7 este descrisa elasticitatea substituirii din punct de vedere geometric:

In punctul initial, raportul dintre inputuri se situeaza in punctul C, iar RMST este data de panta tangentei la izocuanta ce trece prin punctele C si B (respectiv dreapta CB). Daca raportul dintre inputuri se va modifica, ajungand in punctul D, atunci RMST va fi panta tangentei la izocuanta in punctul D, respectiv AD. Elasticitatea substituirii este o masura a curburii , iar este dat de raportul .

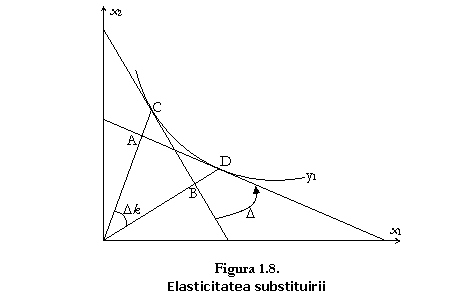
Nu exista un consens in ceea ce priveste indicatorul ce poate masura gradul de substituire intre inputuri.

Cea mai frecventa utilizata definitie este cea a elasticitatii directe a substituirii (care a fost data anterior).

Mai exista insa si alte definitii din care amintim:

Elasticitatea partiala a substituirii a lui Allen

,

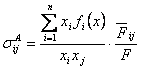unde

- este determinantul matricei Hessiene asociat functiei de productie , bordate cu derivatele partiale de ordinul I.

cu si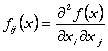

,

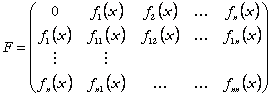Atat elasticitatea directa a substituirii cat si elasticitatea Allen a substituirii sunt masuri simetrice ale gradului de substituire intre doua inputuri.

Pentru o functie de productie cu doar doua inputuri, cele doua masuri sunt egale.

Observatii:

1. Daca elasticitatile substitutiei sunt negative, atunci inputurile sunt complementare, iar daca sunt pozitive, atunci inputurile sunt substituibile.

2. In practica, cel putin una dintre elasticitati trebuie sa fie pozitive, adica un factor de productie nu poate fi complementar cu toti ceilalti.

Elasticitatea substituirii factorilor Morishima:

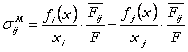
Legatura dintre elasticitatile Morishima si Allen este data de:

Observatii:

- nu este simetrica;

- o pereche de inputuri ar putea fi complementare daca sunt definite prin intermediul masurii Allen, iar prin cel al masurii Morishima - substituibile ( dar );

- daca doua inputuri sunt substituibile conform masurii Allen () atunci intotdeauna ele vor fi substituibile si conform masurii Morishima dar ().

Identificarea functiilor de productie si a progresului tehnic

Cadrul conceptual

Specificul activitatilor fiecarei firme sau calitatea managementului, a structurii tehnice pe categorii si varste de utilaje, calitatea fortei de munca angajate si capacitatea de reactie la factorii de mediu ne conduc la ideea ca exista o mare diversitate de functii de productie, practic fiecare firma avand o functie proprie de productie. Aceasta, nu atat in privinta parametrilor diverselor tipuri de functii - parametrii a caror valoare se estimeaza prin metoda celor mai mici patrate, cat a formei acestor functii, care poate fi specificata prin diferite metode. In practica, cel mai adesea se utilizeaza functia Cobb-Douglas, desi alegerea ei nu are nici un fundament legat de specificul activitatilor cercetate. De aceea, ne propunem sa gasim, in functie de particularitatile acestor activitati forma functiei de productie prin care pot fi specificate, forma care permite aprecierea ca apartine unei anumite clase de functii elementare: functia Cobb-Douglas, functia CES, functia VES, etc.

Metoda identificarii functiei de productie pentru un anumit producator (sau agregat, la nivelul ramurii sau economiei nationale) se fundamenteaza pe cercetarea fenomenologica: determinarea statistica a celor mai stabile corelatii intre indicatorii (medii, marginali, de substitutie si elasticitati) activitatii si pe aceasta baza, deducerea functiei de productie, prin algoritmul:

pasul 1: determinam o corelatie stabila intre indicatori. Aceasta core­latie se exprima printr-o ecuatie diferentiala, in care variabila este, de regula, productivitatea muncii. Aceasta corelatie este o ecuatie diferentiala.

pasul 2: integram aceasta ecuatie si obtinem functia de productie cu sau fara progres tehnic.

Prin metoda identificarii avem posibilitatea deducerii diverselor clase de functii de productie. Pe aceasta baza, in practica, putem folosi doua metode pentru specificarea functiei de productie:

Metoda I: rezulta direct din algoritmul de identificare a functiei de productie, bazat pe cercetarea fenomenologica a corelatiilor fundamentale.

Metoda II: Se utilizeaza N clase de functii de productie cunoscute, cu sau fara progres tehnic (Cobb-Douglas, Cobb-Douglas generalizata, CES, VES, Sato, etc.) si pe baza datelor statistice se alege cea mai buna sub aspectul indicatorilor de testare statistica si a respectarii legitatilor economice fundamentale.

Evident, a doua metoda este mai restrictiva fata de prima, intrucat aplicand prima metoda putem obtine o functie de productie ce nu apartine nici uneia din clasele de functii prestabilite in metoda a doua.

Pentru aplicarea metodei I sintetizam indicatorii functiei de productie in varianta ca este cu randamente constante la scala, adica gradul de omogenitate este , deci verifica cerinta:

.

Luand si notand 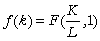unde este inzestrarea tehnica a muncii, deducem ca - este productivitatea medie a muncii, .

Consecinta: functia de productie se determina imediat cunoscand functia f(k), din .

Ceilalti indicatori se deduc din aceasta relatie, conform definitiei lor din 1.3.

- Randamentul mediu al capitalului:

- Indicatori marginali:

- productivitatea marginala

Gasim:

- randamentul marginal al capitalului: Þ

Cum ceilalti indicatori (elasticitati, RMST, coeficientul elasticitatii RMST) se deduc din indicatori medii si marginali, obtinem tabelul indicatorilor:

Tabelul 1

*Consideram r - valoarea absoluta, , cand evident de-a lungul izocuantei Y = fixat, dK > 0, dL<0.

Observatii

1) In cazul general cand gradul de omogenitate este deducem simi­lar, ca functia de productie este .

In consecinta:

- indicatorii medii sunt:

- indicatorii marginali:

Elasticitatile:

RMST: si coeficientul elasticitatii avand aceeasi expresie, dar valoarea dependenta de .

2) Se constata ca fata de cazul particular al functiei omotetice (), in cazul general, indicatorii medii si marginali se obtin din cei corespunzatori acestui caz, prin multiplicarea cu . Este modificata expresia elasticitatii productiei in raport cu munca, in loc de avem si de asemenea RMST este in loc de .

Ca o consecinta, suma elasticitatilor este atat in cazul general cat si in cel particular cand .

Identificarea functiilor de productie
fara progres tehnic

Obiectivul este determinarea expresiei functiei:

Consideram cazul particular cand F este cu randamente constante la scala (). Cazul general nu prezinta dificultati de abordare, fiind posibil studiul in mod similar, conform rezultatelor din observatia 1) de mai sus.

Cercetam cateva variante privind specificarea statistica a corelatiei stabile posibile intre indicatori.

A. Functii induse de forma elasticitatilor

Datele statistice evidentiaza o expresie statistica stabila a elasticitatii in raport cu munca , unde este o functie elementara - liniara, parabolica, hiperbolica, logaritmica, exponentiala, etc., conform metodologiei statistice de specificare, estimare si testare parametrica si de concordanta. Alegerea expresiei h(k) se face in primul rand pe baza distributiei ansamblului de puncte (k, E_L) de-a lungul orizontului statistic (figura 9.a, b).

Conform tabelului, folosind expresia elasticitatii, deducem ecuatia diferentiala:

(1.5.1)

Prin integrare, obtinem:

adica:

(1.5.1')

unde H(k) este primitiva si C = constanta de integrare.

Deducem expresia productivitatii muncii:

si in consecinta, forma functiei de productie

(1.5.1")

Situatii concret posibile:

A1) - deci o dependenta liniara (care cuprinde si cazul h(k) = constant, cand ).

Primitiva

deci

(1.5.1.a)

care este functia Cobb-Douglas generalizata. Se constata ca atunci cand (deci elasticitatea constant, ), se obtine functia Cobb-Douglas clasica.

Asadar, se delimiteaza deja o conditie suficienta de aplicare a functiei Cobb-Douglas si anume cand elasticitatea in raport cu unul din factori este constanta. Daca elasticitatea este liniara cu panta , in raport cu dotarea tehnica per capita, specificarea prin functia Cobb-Douglas nu este corecta, adevarata functie fiind (1.5.1.a).

A2) Dependente neliniare: cazurile cand:

i)

ii) si

iii)

Indicatie: In cazul i) deducem functia de productie

(1.5.1.b)

adica o functie cvasi-Cobb-Douglas cand si

- cand .

ii) Gasim primitiva si ecuatia (1.5.1') ne conduce la functia de productie:

(1.5.1.c)

care este functia Cobb-Douglas cu elaticitati variabile.

iii) Gasim primitiva si functia de productie

(1.5.1.d)

o functie de tip cvasi-Cobb-Douglas.

Observatii

1. Aceeasi metodologie se aplica si in cazul general cand nu pornim cu ipoteza apriori ca functia de productie este cu randamente constante la scala, ci are gradul de omogenitate . Ecuatia (1.5.1) devine:

(1.5.1.g)

care se integreaza.

Studii de caz: reluati situatiile concrete de mai sus privind forma functiei h(k) si refaceti calculele in cazul general, folosind (1.5.1.g). Interpretati rezultatele gasite.

2. Exista o mare diversitate de forme de functii de productie rezultate din forma functiei h(k).

3. Similar se procedeaza daca folosim elasticitatea capitalului . Reluati si in aceasta varianta cercetarea cand h(k) este de tip A₁) sau A₂), liniara sau neliniara.

B. Functii induse de forma randamentelor marginale

Datele statistice evidentiaza dependenta productivitatii marginale de productivitatea medie, . Aceasta dependenta are la baza ideea ca in conditiile deciziei optime (privind maximizarea profitului sau minimizarea costurilor) la firma, gasim*) (unde c_L = salariul nominal - reprezinta costul muncii si multiplicatorul Lagrange). Ori, este binecunoscuta legitatea economica a concordantei intre salariu si productivitatea muncii; in consecinta functia h este monoton crescatoare si concava.

In concluzie, deducem ecuatia diferentiala:

(1.5.2)

cu variabile separabile, care prin integrare devine:

(1.5.2')

Notam G(f(k)) primitiva din stanga si obtinem:

G(f(k)) = ln Ak unde A - constanta de integrare.

Deoarece f(k) > h(f(k)) din continutul economic (productivitatea>salariul) rezulta ca G este monoton crescatoare, deci inversabila (pe codoemniul sau), deci

(1.5.2")

de unde, functia de productie este:

(1.5.2"')

in care c = lnA.

Expresii concrete:

b1) Functia h este liniara: , cu , adica salariul creste proportional cu productivitatea. Gasim:

Deci ecuatia (1.5.2') devine:

(c = constanta)

adica

(A = constanta)

Gasim:

deci functia de productie este:

(1.5.2.a)

adica un tip nou, o combinatie liniara intre Cobb-Douglas si o functie liniara in L. Daca se regaseste Cobb-Douglas.

b2) Functia h este neliniara: , concava. Corespunde ipotezei ca salariul creste o data cu cresterea productivitatii, dar cu un ritm mai mic.

De exemplu, . In acest caz primitiva G va fi:

Deci ecuatia (1.5.2') devine:

(A = constanta)

Expresia productivitatii muncii este in acest caz:

cu

deci functia de productie va fi:

(1.5.2.b)

o forma cu totul neasteptata, provenita dintr-o ipoteza foarte realista.

Propunem ca exercitiu rezolvarea in cazul general*) si particularizarea cand si .

Observatii

1. Similar se poate formula abordarea in cazul genaral cand . Propunem ca studiu de caz analiza in cele doua situatii b₁) si b₂).

Indicatie In cazul cand dependenta este liniara, obtinem ecuatia diferentiala:

si dupa integrare, functia de productie:

(1.5.2.a')

2. O abordare similara se aplica atunci cand se analizeaza corelatia intre randamentul marginal si randamentul mediu al capitalului, , din care deducem ecuatia diferentiala (EDVS)*) cand:

Propunem ca studiu de caz detalierea calculelor si deducerea functiei de productie cand h(w_K) este liniara, respectiv neliniara, de aceleasi forme ca mai sus. Aceeasi procedura, cand .

C. Functii induse de forma RMST

O a treia categorie vizeaza analiza statistica a RMST prin care se evidentiaza dependenta de inzestrarea tehnica:

(1.5.3)

unde, pentru , regasim cazul particular al functiei cu randamente constante la scala. Obtinem:

(1.5.3')

si integrand, rezulta:

(1.5.3")

unde A = constanta si

Functia de productie va fi:

(1.5.3"')

Studiem cazul concret cand:

c1) functia h este liniara:

Deducem:

Deci, conform (1.5.3"), obtinem:

si functia de productie:

(1.5.3.a)

Daca , situatie ce corespunde ipotezei ca RMST =
= constant, care reflecta continutul economic ca la optim 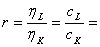constant (indexarea perfecta*) a costurilor factorilor cu rata inflatiei), obtinem:

Pentru , aceasta este o functie liniara de productie, iar , este o functie particulara CES.

c₂) Studiu de caz propus: analizati cazul cand .

D. Functii induse de expresia elasticitatii de substitutie

A patra categorie vizeaza cercetarea pe date statistice a dependentei intre coeficientul elasticitatii de substitutie si inzestrarea tehnica per capita:

, adica         (1.5.4)

Deducem EDVS:

care prin integrare conduce la o expresie a RMST:

(1.5.4')

unde .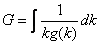

In continuare, intram in tipologia problemei de la punctul anterior c).

d₁) Astfel, in cazul cand constant (adica de tip CES), obtinem:

, deci .

Notam si conform (1.5.3') deducem EDVS:

(1.5.4.a)

Calculam primitiva

, .

Deci (1.5.4.a), B₁ = constanta de integrare. Obtinem:

, unde si functia de productie:

adica

deci binecunoscuta functie CES, daca luam :

(1.5.4.b)

unde si sunt constante (ale caror expresii pot fi obtinute din A si B, dar nu ne intereseaza).

Cazul cand se deduce direct din (1.5.4.a):

adica :

deci o functie Cobb-Douglas (unde - constanta).

Deducem concomitent si urmatoarea legitate:

Daca elasticitatea RMST, , functia CES devine o functie Cobb-Douglas. Deci functia Cobb-Douglas este un caz particular al functiei CES.

d₂) Daca constant, obtinem functii de productie de tip VES (Variable Elasticity of Substitution).

Astfel, functiile de productie de tip Allen si Sato sunt de tip VES. Intr-adevar, pentru functia Allen, avem:

iar pentru functia Sato:

variabile in raport cu dotarea tehnica k, deci de tip VES.

Prin procedura de la punctul b) gasim functia Sato:

si functia Allen:

si .

Invers, pornind de la aceste functii obtinem imediat si .

Specificarea progresului tehnic si identificarea

functiilor de productie
cu progres tehnic neincorporat

Indicatorii progresului tehnic

Problema definirii, a specificarii si cuantificarii progresului tehnic este deosebit de complexa si a generat o bogata literatura de specialitate, incepand cu conceptul de progres tehnic neutral (Hicks-1932), extins la progres tehnic neincorporat (de tip Harrod sau Solow), progres tehnic incorporat (de tip Solow sau Weiszacker), progres tehnic indus (de calitatea factorilor: Nelson sau Denison si de experienta: Arrow).

Intr-o prima abordare, progresul tehnic poate fi considerat ca un factor care genereaza cresterea outputului in timp, chiar daca volumul factorilor fizici (inputurilor) ramane constant pe termen scurt. In consecinta, putem folosi teoria functiilor de productie, introducand ca factor de sine statator, timpul t. Fie functia si ; specificam functia de productie (monoutput) prin:

(1.5.5)

De exemplu, functia neoclasica cu progres tehnic va fi:

(1.5.5')

unde F are proprietatile cunoscute pe - adica pozitivitate, randamente marginale descrescatoare si matricea hessiana negativ (semi)definita, iar in raport cu t are proprietatea .

In consecinta, pe langa indicatorii prezentati in tabelul 1, paragraful anterior si care aici vor fi de forma:

, etc.

deci contin explicit variabila timp, se introduc si doi indicatori specifici pentru a caracteriza efectul direct al celei de-a treia variabile, timpul t, deci a progresului tehnic:

ritmul progresului tehnic:

(1.5.6)

directia progresului tehnic:

(1.5.7)

adica ritmul modificarii in timp a coeficientului de substituire a factorilor (concret a muncii - forta de munca) cu cea materializata (stocul de bunuri de capital). Continutul economic al coeficientului D rezulta din ideea ca in conditiile unui management optimal, avem , adica actiunea interna a firmei de substituire a muncii prin capital (), este indusa de pietele factorilor prin pretul relativ al acestor factori (), deci D comensureaza dinamica modificarii la firma a ratei de substituire () in functie de variatia pretului relativ al factorilor de productie, preturi fixate exogen*) pe pietele acestor factori.

O importanta consecinta a folosirii functiilor de productie cu progres tehnic este aceea ca putem cuantifica ritmul cresterii outputului:

(1.5.8)

adica

- ritmul cresterii productiei este dedus ca o combinatie liniara (convexa - cand functia este cu randamente constante la scala: ) a ritmurilor de crestere a factorilor, la care se adauga direct ritmul cresterii prin progresul tehnic.

Demonstratia este imediata si se deduce din derivata totala a functiei , tinand seama de definitia elasticitatilor.

In aceste conditii, ritmul progresului tehnic are o determinatie endogena prin:

(1.5.6')

deci este o combinatie liniara intre ritmurile de variatie a randamentelor marginale, coeficientii fiind elasticitatile celor doi factori. In consecinta, ritmul de crestere a productiei are o determinare complexa:

(1.5.8')

in care, pe langa ritmul cresterii factorilor, o contributie importanta o are ritmul de variatie al randamentelor marginale a factorilor, iar ponderile contributiilor acestora sunt elasticitatile productiei in raport cu factorii respectivi. Insa, cum in conditiile unui management optimal si trebuie sa raspunda cerintelor induse de preturile factorilor fixate exogen pe pietele respective, ritmul productiei (care este o decizie endogena firmei) este influentat in mare masura de dinamica acestor preturi, ceea ce reflecta un mecanism adaptiv al deciziilor la firma in functie de influentele exogene ale pietelor factorilor.

Identificarea tipului de progres tehnic neincorporat

In literatura de specialitate s-au conturat mai multe directii de cuantificare a progresului tehnic, dupa diverse criterii:

daca factorii de productie sunt comensurati agregat, in sensul ca nu tinem seama de diversele generatii din care provin, progresul tehnic este de tip neincorporat pe generatii de factori; in caz contrar, spunem ca specificarea este de tip progres tehnic incorporat (vezi mai jos, modelele de tip Solow, respectiv Weizacker);

daca progresul tehnic actioneaza in mod egal asupra factorilor de productie, lasand neschimbat (invariant) raportul randamentelor marginale ale factorilor, adica RMST - este invarianta in timp, avem de a face cu un progres tehnic neutral (in sens Hicks);

daca progresul tehnic actioneaza in principal prin capital, efectul este cresterea randamentului marginal al acestuia, in detrimentul productivitatii muncii si in consecinta acest tip de PT este generator de economie de munca vie (este tip progres tehnic neincorporat - PTN de tip Solow);

daca actiunea este inversa, cand PT este generator de economie de capital, avem PTN de tip Harrod.

In consecinta, identificarea progresului tehnic de tip neincorporat sau neutral se fundamenteaza pe ideea ca anumiti indicatori sunt invarianti in timp, o idee foarte importanta pentru ca introduce si in problematica economica un mecanism specific stiintelor exacte, acela al identificarii unor invarianti.

A. Progres tehnic neutral de tip Hicks

Se fundamenteaza pe ipoteza ca RMST este invarianta in timp si depinde numai de dotarea tehnica per capita:

(1.5.9)

Obtinem ecuatia diferentiala:

(1.5.9')

care prin integrare, da:

(1.5.9")

unde - este o primitiva a membrului din dreapta al ecuatiei (1.5.9') si constanta de integrare este in acest caz o functie de timp c(t) si constanta in raport cu variabila de integrare k_t. Obtinem expresia productivitatii:

si functia de productie:

(1.5.9"')

unde si , deci ritmul progresului tehnic este si in consecinta functia de productie cu PTN Hicks este:

(1.5.9"'.a)

Asadar, PTN Hicks actioneaza concomitent prin cei doi factori si nu potenteaza doar unul dintre ei.

B. Progres tehnic neincorporat de tip Solow

Are la baza ideea ca randamentul marginal al muncii este invariant in timp, dar depinde de productivitatea medie a muncii:

(1.5.10)

Economic, aceasta cerinta reflecta un comportament rational al angajatorului privind negocierea salariului, in functie de productivitatea realizata de angajat, indiferent de momentul de timp (in ianuarie sau in decembrie, in anul acesta sau in anii urmatori). Aici trebuie observat ca efectul inflatiei in comensurarea indicatorilor se transmite prin nivelul nominal al productivitatii muncii, .

Inlocuind indicatorii din (1.5.10) cu expresiile lor, deducem EDVS:

(1.5.10')

care prin integrare conduce la:

unde A(t) este constanta de integrare (fata de variabila k_t) si

Din (1.5.10') deducem expresia productivitatii muncii:

(1.5.10")

deci functia de productie cu PTN de tip Solow este:

(1.5.10"')

care evidentiaza clar ca PT actioneaza prin intermediul capitalului, deci este generator de munca vie.

C. Progres tehnic neutral de tip Harrod

Are la baza ipoteza invariantei in timp a randamentului marginal al capitalului, dar depinde numai de randamentul mediu al acestuia:

(1.5.11)

Se obtine ecuatia diferentiala:

(1.5.11')

care prin integrare conduce la functia de productie:

(1.5.11")

si evidentiaza ca PT actioneaza prin intermediul muncii, fiind generator de capital. Acesta este PTN de tip Harrod.

Acestea sunt variantele devenite clasice ale progresului tehnic neincorporat factorilor. Insa, pe acelasi rationament al invariantei in timp al unor indicatori si dependenta acestora de alti indicatori se deduc o multitudine de functii de productie cu progres tehnic, de exemplu:

etc.

D. Studii de caz

Identificati functia de productie si tipul progresului tehnic cand:

a)    RMST este invarianta in timp, dar dependenta liniar de inzestrarea tehnica: .

b)   Aceeasi problema cand .

c)    Productivitatea marginala este invarianta in timp, dar depinde liniar de productivitatea muncii: .

d)   Aceeasi problema, dar dependenta este neliniara:

si concret,

e)    Randamentul marginal al capitalului este invariant in timp si este dependent liniar de randamentul mediu:

f)     Aceeasi problema, dar dependenta este neliniara:

g)    Coeficientul elasticitatii de substitutie este invariant in timp, dar depinde liniar de dotarea tehnica per capita:

h)    Elasticitatea in raport cu munca este invarianta in timp, dar este dependenta de dotarea tehnica per capita, dependenta fiind:

unde h(k_t) sunt specificate prin expresiile i), ii), iii) de la punctul a₂) din paragraful 1.5.2.

Indicatie

a) conduce la EDVS (1.5.9') care prin integrare da:

adica:

unde .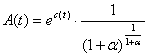

Functia de productie va fi:

unde:

deci progresul tehnic este neutral, de tip Hicks.

b) Deducem ecuatia primitiva din membrul drept este o integrala binoma de tip Cebasev, deci facem schimbarea de variabila si dupa calculele elementare gasim:

deci functia de productie este:

adica de tip CES, cu PTN de tip Hicks.

Observatie Pentru , regasim cazul de la a).

c) Procedand ca la punctul b₁) din paragraful 1.5.2, cu observatia ca vom lua constanta de integrare c(t), deducem functia de productie:

(1.5.2.a')

unde - constante , deci progresul tehnic este de tip Solow (potenteaza numai capitalul).

d) Obtinem ecuatia diferentiala (1.5.10') si integrand, in membrul din stanga avem o integrala de tip Cebasev, ca la punctul b) de mai sus si facem schimbarea de variabila . Se continua calculele ca mai sus.

Procedand similar, propunem rezolvarea celorlalte puncte; vom mai zabovi asupra cazului f) care conduce la ecuatia:

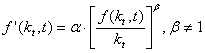
adica:

adica:

deci functia de productie este:

, de tip CES, cu PTN Harrod.

Din scurta prezentare facuta in paragrafele 1.5.2 si 1.5.3 se deduce ca exista o mare varietate de functii de productie pe care se implanteaza cele trei forme de progres tehnic neincorporat:

de tip Hics:

de tip Solow:

de tip Harrod: ,

oricare ar fi forma functiei identificata ca in 1.5.2.

Trebuie insa observat ca singura functie de productie pentru care tipul de progres tehnic poate fi atat de tip Hicks, de tip Solow sau de tip Harrod este functia Cobb-Douglas:

.

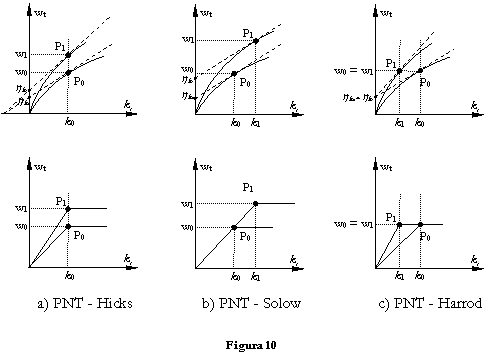
Efectele actiunii celor trei tipuri de progres asupra dinamicii productivitatii muncii si a randamentului marginal al capitalului sunt ilustrate in figura 10, intr-o reprezentare paralela - pentru functii de productie cu factori substituibili, respectiv cu factori complementari, pentru doua momente de timp t₀ si t₁, t₀<t₁. Punctele in care sunt calculati indicatorii la cele doua momente de timp sunt P₀ si P₁.

Specificarea progresului tehnic incorporat

Modelele prezentate anterior ale PTN evidentiaza efectele actiunii PT prin volumul agregat al factorilor K_t sau L_t. In realitate, actiunea PT este diferita pe generatii de factori; de exemplu, capitalul corporal din generatii mai noi incorporeaza progresul tehnologic al ultimelor descoperiri in cercetarea stiintifica si tehnologica, deci isi aduce un aport mai ridicat in cresterea productivitatii fata de acelasi volum al capitalului din generatii mai vechi. Similar, pentru generatiile mai noi de forta de munca care aplica cunostintele (teoretice si practice) cele mai recente in domeniul de specializare in care au fost formati, in special capacitatea de utilizare a noilor tehnologii informatizate si o mai mare adaptabilitate la fluxul informational foarte dinamic al prezentului si viitorului.

Progresul tehnic incorporat capitalului. Modelul Solow al PTI

Pentru un sistem economic (firma, ramura, economie nationala) notam - volumul capitalului detinut la momentul curent t si pus in functiune la momentul si - forta de munca care isi desfasoara activitatea pe utilaje din generatia . Volumul productiei realizate va fi cuantificat prin functia de productie cu PTN de tip Solow, - dupa metodologia de mai sus.

Volumul productiei (outputul) creat la momentul t este suma productiilor realizate cu capitalul fix din diverse generatii, fiind varsta celei mai vechi generatii de bunuri de capital detinut de firma (ramura, etc.). Deci in ipoteza utilizarii unui model continuu in timp,

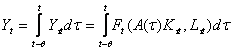(1.5.12)

si in cazul modelului discret, avem:

(1.5.13)

Functia de productie poate fi oricare din formele specificate in paragrafele anterioare, dar pentru simplificarea abordarii vom folosi functia Cobb-Douglas cu ritmul progresului tehnic - constant, deci , A=constanta.

Tinand cont de rata deprecierii capitalului fix, volumul existent la momentul curent din total capital pus in functiune la momentul este: , unde - investitiile facute la momentul trecut .

In aceste conditii, volumul outputului va fi:

si in consecinta, volumul productiei realizat la momentul curent este:

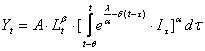(1.5.12')

unde L_t este volumul fortei de munca utilizat la momentul t. In consecinta, in model nu este necesar sa determinam efectiv forta de munca utilizata pe diverse generatii de capital, operatie care practic poate fi deosebit de dificila.

In modelul discret, abordarea este similara, dar ritmurile (progresului tehnic respectiv deprecierii capitalului) vor fi utilizate conform modelarii discrete, de tip deci . In consecinta, progresul tehnic va fi , A - constanta si efectul deprecierii capitalului este cuantificat prin , deci functia de productie este:

(1.5.13')

In concluzie, modelul Solow cu progres tehnic incorporat pe generatii de capital pune in evidenta rolul investitiilor ca purtatoare ale progresului tehnic precum si influenta deprecierii capitalului fix.

Trebuie insa observat ca pe langa progresul tehnic incorporat pe generatii de capital, pe care in model l-am introdus prin ritmul , actioneaza si un progres tehnic autonom, neincorporat, generat la momentul curent de managementul intregului sistem (organizarea productiei, a muncii, activitatea de marketing, financiara, etc). Introducem acest PTN prin ritmul constant si actioneaza in modelele anterioare (1.5.12'), (1.5.13') prin expresia A(t) in loc de A cu respectiv .

Se obtine modelul Solow cu doua trenduri ale PT:

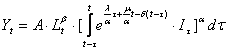(1.5.12")

in cazul continuu, respectiv:

(1.5.13")

B. Progresul tehnic incorporat fortei de munca.

Modelul Weiszacker

Se fundamenteaza printr-o abordare similara cu PTI capitalului, de data aceasta pornind de la ideea ca fiecare generatie de forta de munca isi aduce contributia in mod diferentiat la cresterea productiei. Fie - numarul persoanelor in activitate la momentul curent t avand vechimea de la angajare (considerata imediat dupa terminarea studiilor de formare in specialitatea dorita) si indicele de eficienta a unui angajat din categoria . In consecinta, la momentul t, volumul fortei de munca va fi:

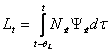, respectiv   (1.5.14)

Exista mai multe metode de cuantificare a indicelui (metode statistice, metoda punctajului s.a.), dar Weiszacker propune specificarea acestor indici in functie de nivelul de calificare exprimat in ani de studii (cuprinzand inclusiv durata studiilor suplimentare de perfectionare), de gradul de depreciere a cunostintelor o data cu trecerea timpului, fata de momentul formarii si de experienta capatata prin munca si in formarea permanenta ("learning by doing"- dupa Arrow). In aceste conditii putem scrie cu - prin care se reflecta gradul de depreciere si sausau dupa cum abordarea se face in timp continuu respectiv discret.

Combinand aceste rezultate cu modelele de la punctul A) deducem modelul (continuu sau discret) cu trei trenduri ale progresului tehnic:

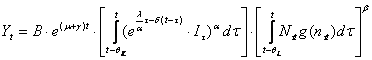(1.5.14')

respectiv:

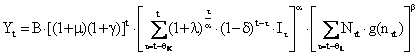
unde B - constanta, - varsta celei mai vechi generatii de bunuri de capital, - varsta celei mai vechi generatii de forta de munca.

C. Progresul tehnic incorporat prin calitatea factorilor
(Denison - Nelson)

Functia de productie este specificata prin:

(1.5.15)

unde este volumul potential al capitalului, respectiv al fortei de munca.

Denison face ipoteza ca variatia volumului potential al capitalului are loc sub influenta a trei factori, deci:

(1.5.16)

unde primul termen reprezinta ritmul de crestere al capitalului K_t; al doilea contine prima componenta - reprezentand ritmul progresului tehnic incorporat capitalului si a doua - care reflecta efectul modificarii structurii capitalului si a duratei medii de functionare, (reducerea duratei medii de amortizare).

Similar, pentru forta de munca, Nelson porneste de la constatarea ca variatia potentialului de munca este:

(1.5.17)

primul termen reprezentand factorul cantitativ, prin ritmul cresterii volumului fizic de munca;

al doilea este factorul calitativ, reflectand ritmul progresului tehnic incorporat fortei de munca prin cresterea nivelului de pregatire in specialitate, prin experienta in munca si informatizarea activitatilor desfasurate.

In concluzie, ritmul de crestere a productiei va fi (conform 1.5.8):

(1.5.8')

unde ritmul progresului tehnic este:

(1.5.16')

in care - este ritmul progresului tehnic autonom.

Aceasta scurta prezentare a modalitatilor de specificare a progresului tehnic are, in opinia noastra, obiectivul de a deschide pentru cititor caile de dezvoltare mai aprofundata asupra acestei problematici deosebit de complexa, dar si foarte importanta.