
| MANAGEMENT
Termenul Management a fost definit de catre Mary Follet prin expresia "arta de a infaptui ceva impreuna cu alti oameni". Diferite informatii care te vor ajuta din domeniul managerial: Managementul Performantei, Functii ale managementului, in cariera, financiar. |
| StiuCum
Home » MANAGEMENT
» managementul investitiilor
|
||||||||||||||||||||||||||||
Mecanisme de reglare fundamentate pe teoria costurilor firmei |
||||||||||||||||||||||||||||
|
Mecanisme de reglare fundamentate pe teoria costurilor firmei In teoria economica au fost fundamentate numeroase concepte privind costurile firmei, cum ar fi: cost contabil, cost de oportunitate, social sau alternativ, cost economic. Fata de costul contabil, definit ca suma de cheltuieli de productie, calculate pe baza preturilor de achizitie, ale factorilor de productie, tarifelor pentru manopera si a amortizarilor, costul de oportunitate (social sau alternativ), reprezinta plata necesara pentru a mentine o resursa in utilizarea ei prezenta, tinand seama de posibilitatea utilizarii alternative a factorilor de productie. Spre deosebire de costul contabil, exprimat in unitati monetare, costul de oportunitate se exprima ca rata de scont a sumei avansata pentru achizitionarea factorilor de productie. Costul economic este un concept care are la baza costul de oportunitate si care ia in plus in considerare efectele externe sau externalitatile (beneficiile sau pierderile generate de activitatea altor agenti economici sau procesele care au loc in mediul inconjurator). Formalizarile urmatoare au in vedere in special costul contabil care permite estimari econometrice pentru identificare. Definirea functiei de cost. Tipuri de functii de costPrin definitie, functia de cost total este solutia problemei de optimizare: (1)
Din definitia (1) rezulta ca functia de cost este cheltuiala minima (date fiind preturile factorilor de productie / pentru producerea unui nivel al productiei finite. In relatia (1), preturile
factorilor sunt date exogen (se face ipoteza competitiei perfecte). Vom
presupune, de asemenea, ca nu exista factori de productie cu preturi zero Observam ca functia de cost
definita prin (1) depinde de tehnologie prin restrictia tehnologica Definim: (2) (3) Costurile medii sau unitare ale firmei sunt: (4) (5) (6) (7) Proprietatile functiei de costFunctia de cost definita prin (1), trebuie sa satisfaca urmatoarele proprietati: a. Conform acestei proprietati, nu este posibil a se produce un output pozitiv cu un cost nul. Ca o consecinta a proprietatii de esentialitate stabila a functiei de productie (orice nivel de productie finita - output - este obtinut prin utilizarea unei cantitati strict pozitive din cel putin un input - factor de productie). Intrucat preturile pietei sunt strict pozitive (factorii de productie nu au disponibil liber), costul total va fi strict pozitiv. b. Daca Demonstratie: Consideram
Adunand cele doua relatii obtinem:
Relatia (8) este inegalitatea fundamentla a minimizarii costurilor folosita in statica comparata. Scrisa pe componente, relatia (8) devine:
ceea ce releva faptul ca modificarea pretului unui input va atrage modificarea in directie opusa a 656f56g utilizarii inputului, respectiv functiile de cerere derivata (cererea de factori de productie) sunt descrescatoare in preturi. c. Consideram
Pentru de demonstra concavitatea, trebuie sa aratam ca:
Consideram
Putem scrie:
d. Aceasta este binecunoscuta proprietate numita "absenta iluziei monetare" ceea ce permite utilizarea preturilor relative in functiile de cost. Conform acestei proprietati rezulta ca variatia proportionala a preturilor de intrare, va duce la modificarea functiei de cost in aceeasi proportie.
e. Daca Rezulta, conform acestei proprietati ca o crestere a nivelului outputului (a productiei finite), nu poate duce la descresterea costurilor. Consideram f. Functia de cost satisface lema lui Shephard: daca
respectiv, scris pe componente:
unde
Figura 1 reflecta situatia in
care exista o infinitate de combinatii intre Functia de cost polinomialaExista multe cazuri, in teoria microeconomica
in care se foloseste functia de cost polinomiala Fara sa contrazica rezultatele anterioare, pentru functia polinomiala au fost dezvoltate proprietati specifice, pe care le vom formula, unele fara demonstratie. Corelatii
fundamentale intre functiile de cost mediu
|
||||||||||||||||||||||||||||
 |
![]() - constant (29)
- constant (29)
Putem ilustra acum relatia intre
functiile de cost si monotonia veniturilor marginale, exprimate in functie de
productie. Presupunem[*]
![]() , in acest caz
, in acest caz ![]() , adica costurile variabile sunt egale cu costurile totale.
, adica costurile variabile sunt egale cu costurile totale.
Putem observa ca pe termen scurt,
costul total pentru producerea unui anumit nivel al productiei finite nu este
intotdeauna minimal, inrucat depinde de nivelul costurilor fixe. Consideram o
tehnologie cu doua inputuri ![]() (capital tehnic),
(capital tehnic), ![]() (forta de munca), vezi
figura 5. Rezulta:
(forta de munca), vezi
figura 5. Rezulta:
![]() fixat pe termen scurt
fixat pe termen scurt
![]()
![]()
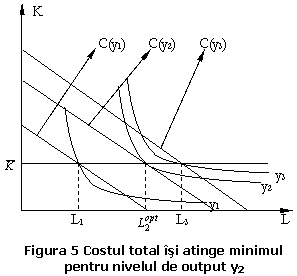 |
In teoria economica conceptele de termen lung si scurt nu sunt definite ca numar aproximativ de ani in evolutia firmei ci mai degraba in raport cu rata de modificare a activelor firmei; astfel termen lung este o durata in care firma isi poate dezvolta stocul de echipamente, tehnologii, piete de desfacere, astfel incat toate costurile pot deveni dependente de volumul productiei. In consecinta termen scurt este o durata de timp in care firma nu-si poate dezvolta tehnologia sau echipamentele, singura posibilitate de a-si creste productia ca urmare a cresterii cererii pe piata, este aceea de a livra din stoc, intrucat nu are timp sa-si procure noi factori de productie, sa-si angajeze noi muncitori, sa-si procure noi tehnologii.
Revenind la definitia functiei de
cost (1), o parte h, din factorii de productie, au durata
indelungata de folosinta, de exemplu elementele de capital fix, in timp ce ![]() factori de productie
ii vom presupune "variabili" in sensul ca sunt inlocuiti (capitalul circulant)
sau retribuiti in urma fiecarui ciclu de productie.
factori de productie
ii vom presupune "variabili" in sensul ca sunt inlocuiti (capitalul circulant)
sau retribuiti in urma fiecarui ciclu de productie.
Presupunem ![]() preturile medii ale
factorilor de productie,
preturile medii ale
factorilor de productie, ![]() factori de productie
cu durata indelungata de folosinta si
factori de productie
cu durata indelungata de folosinta si ![]() factori de productie
"variabili",
factori de productie
"variabili", ![]() rata de scont.
rata de scont.
Costul de oportunitate pentru
factorul ![]() , in perioada
, in perioada ![]() tinand seama de
valoarea actuala a acestora va fi:
tinand seama de
valoarea actuala a acestora va fi:
![]() (
(![]() este numarul de perioade pana la atingerea nivelului minim
al costurilor pe termen lung).
este numarul de perioade pana la atingerea nivelului minim
al costurilor pe termen lung).
Putem acum rescrie definitia (1), tinand seama de structura vectorului inputurilor:
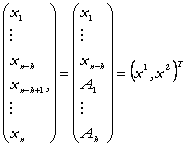
si al preturilor:
![]()
![]() (30)
(30)
unde u este vectorul de componente ui.
Consideram initial doua inputuri,
![]() si
si ![]() , in care
, in care ![]() este restrictionat,
respectiv contine elemente de capital fix.
este restrictionat,
respectiv contine elemente de capital fix.
Costul total pe termen scurt este suma dintre costul total variabil si costul total fix:
![]() (31)
(31)
unde costul total variabil este definit de relatia (1).
Costul total pe termen lung este, conform (31):
![]() (32)
(32)
Rezulta ca problema de minimizare a costurilor pe termen lung este descompusa in doua etape:
a) minimizarea costurilor
variabile pe termen scurt, dandu-se ![]() ;
;
b) alegerea nivelului inputului ![]() care minimizeaza
costul total pe termen lung
care minimizeaza
costul total pe termen lung
Rezulta:
![]() (33)
(33)
si
![]() , (34)
, (34)
unde ![]() este solutia problemei
(32).
este solutia problemei
(32).
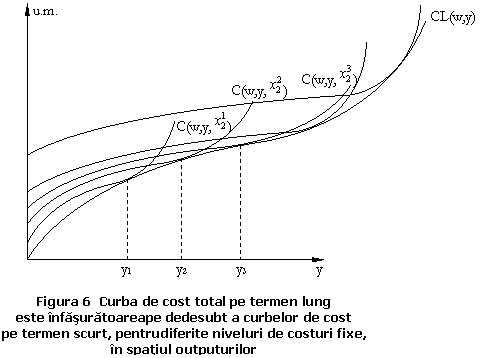
Din (33) si (34) rezulta ca CL![]() este infasuratoarea pe dedesubt a functiilor de cost pe
termen scurt
este infasuratoarea pe dedesubt a functiilor de cost pe
termen scurt ![]() , atat in spatiul preturilor, cat si in spatiul outputului.
, atat in spatiul preturilor, cat si in spatiul outputului.
Din (33) rezulta ca ![]() este limita inferioara
a costurilor fixe pe termen scurt. Din (33) si (34) rezulta, de asemenea, ca
curbele costurilor pe termen scurt si lung nu se pot intersecta niciodata, nici
in spatiul preturilor, nici in spatiul outputurilor, ci sunt tangente.
este limita inferioara
a costurilor fixe pe termen scurt. Din (33) si (34) rezulta, de asemenea, ca
curbele costurilor pe termen scurt si lung nu se pot intersecta niciodata, nici
in spatiul preturilor, nici in spatiul outputurilor, ci sunt tangente.
Semnificatia economica a faptului
ca graficul functiei de cost total infasoara pe dedesubt graficele curbelor pe
termen scurt este foarte importanta. Din proprietatile functiilor de cost, atat
![]() , cat si
, cat si ![]() sunt concave in
preturile factorilor. Prin faptul ca
sunt concave in
preturile factorilor. Prin faptul ca ![]() este deasupra
este deasupra ![]() inseamna ca ele sunt
tangente intr-un punct, sa zicem
inseamna ca ele sunt
tangente intr-un punct, sa zicem ![]() , iar
, iar ![]() este mai concava decat
este mai concava decat
![]() .
.
Conditia de tangenta este:
![]() (35)
(35)
Prin aplicarea temei lui Shephard, (35) devine:
![]() (36)
(36)
Din (36) rezulta ca cererile
derivate pe termen lung si scurt pentru factorul de productie i sunt
egale. Mentionam ca (35) si (36) sunt satisfacute pentru ![]() si
si ![]() respectiv pentru
nivelul costurilor fixe pe termen scurt, care minimizeaza costul total pe
termen lung.
respectiv pentru
nivelul costurilor fixe pe termen scurt, care minimizeaza costul total pe
termen lung.
Faptul ca ![]() este mai concava decat
este mai concava decat
![]() , implica:
, implica:
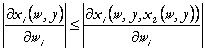 (37)
(37)
Rezulta ca cererea derivata pe termen lung, este mai elastica in raport cu pretul decat cererea derivata pe termen scurt.
Relatia (37) releva principiul Chatelier-Samuelson, care joaca un rol important in teoria microeconomica.
Definim vectorul de inputuri:
![]() (38)
(38)
unde :
![]() subvectorul inputurilor variabile
subvectorul inputurilor variabile
![]() subvectori de inputuri
fixe
subvectori de inputuri
fixe
Presupunem ca inputurile fixe sunt modificate succesiv, generand costuri pe termen foarte scurt:
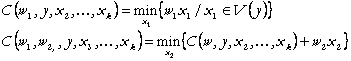
In general:
![]() (39)
(39)
Functia de cost pe termen lung este:
![]() (40)
(40)
Definind costul pe termen scurt ca suma intre costul variabil si costul fix, obtinem:
![]() (41)
(41)
Aceasta succesiune de probleme de minimizare implica:
![]() (42)
(42)
si
![]() (43)
(43)
![]() (multimea indicilor
asociati inputurilor variabile)
(multimea indicilor
asociati inputurilor variabile)
Din (43) rezulta ca, cu cat sunt mai putine inputuri fixe in procesul de productie, modificarea inputurilor variabile indusa de modificarea propriului pret este mai mare.
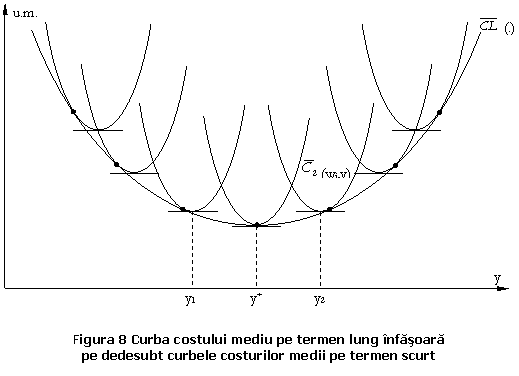
Curba costului mediu pe termen lung infasoara pe dedesubt curbele costurilor medii pe termen scurt.
Lema: Costul
mediu pe termen lung este egal cu costul mediu pe termen scurt pentru nivelul
de output ![]() pentru care costul
total mediu pe termen lung este minim.
pentru care costul
total mediu pe termen lung este minim.
Numim scala de fabricatie nivelul outputurilor care pot fi produse cu un anumit nivel al capitalului (factor de productie cu durata indelungata de folosinta).
Scala optima de fabricatie este nivelul outputurilor care pot fi produse cu un volum al factorilor ficsi (de folosinta indelungata, in special capitalul fix) care minimizeaza costul total pe termen lung.
Notam:
![]() costul mediu pe termen
lung
costul mediu pe termen
lung
![]() costul marginal pe
termen lung
costul marginal pe
termen lung
![]() (44)
(44)
este valabila numai pentru scala optima de fabricatie, y *.
Curba ![]() poarta numele de curba
de planificare, intrucat ea reliefeaza posibilitatile cost-nivel al
productiei firmei la un moment dat.
poarta numele de curba
de planificare, intrucat ea reliefeaza posibilitatile cost-nivel al
productiei firmei la un moment dat.
Lema: Pentru
![]() , nivelul outputului pentru care costul mediu pe termen scurt
si costul mediu pe termen lung sunt minime, costurile marginale pe termen lung
si scurt sunt egale.
, nivelul outputului pentru care costul mediu pe termen scurt
si costul mediu pe termen lung sunt minime, costurile marginale pe termen lung
si scurt sunt egale.
![]() (45)
(45)
Conditia de tangenta a costurilor medii pe termen lung si scurt este:
![]() (46)
(46)
![]() (47)
(47)
Corespunzator:
![]() (48)
(48)
Multiplicam
relatia (46) cu ![]() :
:
![]() (49)
(49)
Adunam (44) cu (49) si obtinem:
![]() (50)
(50)
Membrul stang al relatiei (50)
este ![]() , iar membrul drept este
, iar membrul drept este ![]() . Rezulta ca (45) este verificata.
. Rezulta ca (45) este verificata.
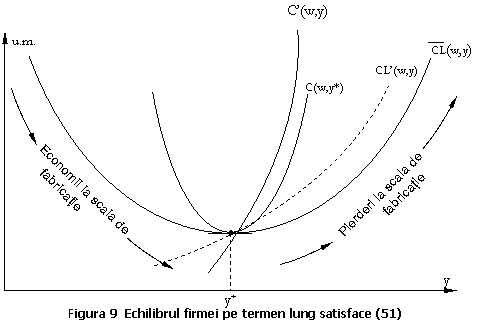
Din fig. rezulta ca scala optima de fabricatie corespunde
![]()
Din prezentarea de mai sus putem trage concluzia ca:
![]() (51)
(51)
Spunem ca firma realizeaza economii
la scala de fabricatie atunci cand curba costului mediu pe termen lung ![]() este descrescatoare,
pe masura ce outputul creste, iar curba costului marginal pe termen lung se
situeaza sub curba costului mediu pe termen lung.
este descrescatoare,
pe masura ce outputul creste, iar curba costului marginal pe termen lung se
situeaza sub curba costului mediu pe termen lung.
Rezulta:

Spunem ca firma poseda pierderi la scala de fabricatie atunci cand curba costului mediu pe termen lung este crescatoare, pe masura ce outputul creste, iar curba costului marginal pe termen lung se situeaza deasupra curbei costului mediu pe termen lung.
Rezulta:

Economiile si pierderile la scala pot fi interne, in cazul in care preturile factorilor raman constante, cand firma se deplaseaza de-a lungul traiectoriei de dezvoltare a firmei (in cazul industriilor cu cost constant); sau externe atunci cand pe termen lung preturile factorilor se modifica (cazul industriilor cu cost crescator sau descrescator).
Ne punem problema sa aratam ca elasticitatea substitutiei factorilor se poate determina direct din functiile de cost.
Conditiile marginale din problema minimizarii costurilor sunt:
![]() (52)
(52)
unde ![]() este functia de
productie cu factori substituibili,
este functia de
productie cu factori substituibili,
![]()
Elasticitatea directa a substitutiei Hickes este:
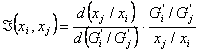 (53)
(53)
Aplicam (52), obtinem:
 (54)
(54)
Am
notat cu ![]() , respectiv
, respectiv ![]()
Din (54) rezulta ca ![]() poate fi interpretat
ca elasticitatea raportului intre inputuri (inputuri relative), in functie de
raportul intre preturile factorilor.
poate fi interpretat
ca elasticitatea raportului intre inputuri (inputuri relative), in functie de
raportul intre preturile factorilor.
Aplicand in continuare lema lui
Shepard, putem exprima ![]() si
si ![]() in functie de
in functie de ![]() .
.
Rezulta ca ![]() da un raspuns al
modificarii procentuale a inputurilor relative in raport cu modificarea cu 1% a
preturilor relative.
da un raspuns al
modificarii procentuale a inputurilor relative in raport cu modificarea cu 1% a
preturilor relative.
Putem deci folosi.![]() pentru a masura modificarea inputurilor indusa de
modificarea preturilor.
pentru a masura modificarea inputurilor indusa de
modificarea preturilor.
Identificam trei tipuri de elasticitati ale substitutiei factorilor:
- elasticitatea substitutiei un
pret / un factor (ESUU) care masoara modificarea procentuala a unui singur
factor, indusa de modificarea unui singur pret ![]()
- elasticitatea substitutiei un pret, doi factori (ESUD), care masoara modificarea procentuala a doi factori, indusa de modificarea unui singur pret:
![]()
- elasticitatea substitutiei,
doua preturi, doi factori (ESDD), care masoara procentual modificarea a doi
factori, indusa de modificarea a doua preturi 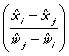 .
.
Diferentiem conditiile de ordinul intai ale problemei de minimizare a costurilor:
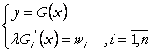 (55)
(55)
![]() multimea inputurilor
admisibile. Trecand la scrierea matriceala obtinem:
multimea inputurilor
admisibile. Trecand la scrierea matriceala obtinem:
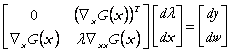 (56)
(56)
unde:
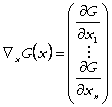 este gradientul
functiei de productie;
este gradientul
functiei de productie;
![]() - matricea Hessian
atasata functiei de productie.
- matricea Hessian
atasata functiei de productie.
In (56) matricea:
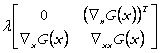 (57)
(57)
este matricea Hessian bordata
Putem determina modificarile cererilor derivate de factori in raport cu preturile factorilor din (56), aplicand regula lui Cramer:
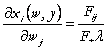 (58)
(58)
unde ![]() este cofactorul
(minorul cu semn) al elementului
este cofactorul
(minorul cu semn) al elementului ![]() al matricei Hessiene
bordate atasata functiei de productie
al matricei Hessiene
bordate atasata functiei de productie ![]() si
si ![]() este determinantul
Hessienei bordate.
este determinantul
Hessienei bordate.
Elasticitatea substitutiei Allen:
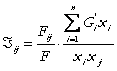 (59)
(59)
Inlocuind (58) in (59) obtinem:
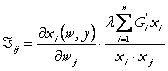 (60)
(60)
In (60) inmultim si impartim
membrul drept cu ![]() ,
obtinem:
,
obtinem:
 (60')
(60')
In (60') 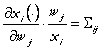 este elasticitatea
cererii derivate de factor
este elasticitatea
cererii derivate de factor ![]() in raport cu pretul
factorului
in raport cu pretul
factorului ![]() .
.
Obtinem:
![]() (61)
(61)
Notam ![]() , ponderea cheltuielilor cu factorul j in totalul
cheltuielilor de productie.
, ponderea cheltuielilor cu factorul j in totalul
cheltuielilor de productie.
Rescriem (61) ca:
![]() (61')
(61')
Din (61') rezulta ca
elasticitatea substitutiei Allen este raportul intre elasticitatea cererii
derivate de factor ![]() in raport cu pretul
produsului
in raport cu pretul
produsului![]() si ponderea cheltuielilor cu factorul
si ponderea cheltuielilor cu factorul![]() in costul total al productiei. Elasticitatea substitutiei
Allen este ESUU.
in costul total al productiei. Elasticitatea substitutiei
Allen este ESUU.
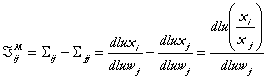 (62)
(62)
In (62) au folosit faptul ca 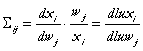
![]() , factorii de productie
, factorii de productie ![]() si
si ![]() sunt Allen substituibili
sunt Allen substituibili
![]() , factorii de productie
, factorii de productie ![]() si
si ![]() sunt Allen complementari
sunt Allen complementari
![]() , factorii de productie
, factorii de productie ![]() si
si ![]() sunt Morishima substituibili
sunt Morishima substituibili
![]() , factorii de productie
, factorii de productie ![]() si
si ![]() sunt Morishima complementari
sunt Morishima complementari
Daca inputurile sunt
substituibili in sens Allen, cresterea pretului inputului ![]() , duce la cresterea nivelului de utilizare a factorului
, duce la cresterea nivelului de utilizare a factorului![]() . Daca inputurile sunt complementare in sens Allen, cresterea
pretului inputurilor
. Daca inputurile sunt complementare in sens Allen, cresterea
pretului inputurilor ![]() , duce la scaderea nivelului de utilizare a factorului
, duce la scaderea nivelului de utilizare a factorului ![]() .
.
Din omogenitatea de grad zero a functiilor de cerere derivata:
![]() (64)
(64)
Impartim ecuatia (64) la ![]() , obtinem:
, obtinem:
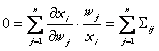 (64')
(64')
Din (64') rezulta:
![]() (65)
(65)
Dar ![]() , ceea ce inseamna ca nici un input nu poate fi complementar
cu toate celelalte inputuri.
, ceea ce inseamna ca nici un input nu poate fi complementar
cu toate celelalte inputuri.
Desi ![]() , incat obtinem ca in elasticitatea substitutiei Allen factorii
substituibili sau complementari se pastreaza, fie ca se utilizeaza
, incat obtinem ca in elasticitatea substitutiei Allen factorii
substituibili sau complementari se pastreaza, fie ca se utilizeaza ![]() sau
sau ![]() .
.
Inputurile ![]() si
si ![]() sunt substituibile Morishima daca si numai daca cresterea lui
sunt substituibile Morishima daca si numai daca cresterea lui
![]() face ca raportul
face ca raportul ![]() sa creasca. Rezulta ca, daca bunurile sunt substituibile
Allen, ele vor fi substituibile si Morishima.
sa creasca. Rezulta ca, daca bunurile sunt substituibile
Allen, ele vor fi substituibile si Morishima.
Ca si in masura Allen, un input nu poate fi complementar Morishima cu toate celelalte inputuri.
Insumam dupa ![]() din (62):
din (62):
![]() , (66)
, (66)
intrucat
![]()
Elasticitatea Morishima nu este
simetrica in semn, ![]() , astfel incat clasificarea in substituibile si complementare
Morishima depinde esential de pretul care se modifica.
, astfel incat clasificarea in substituibile si complementare
Morishima depinde esential de pretul care se modifica.
Consideram ca se modifica
simultan preturile a doi factori ![]() si
si![]() ,
, ![]()
![]() .
.
Scriem diferentiala totala a
functiei ![]() :
:
![]() (67)
(67)
Impartim (67) la ![]() :
:
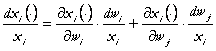 (67')
(67')
In ansamblul drept din (67')
inmultim si impartim primul termen la ![]() , iar al II-lea termen la
, iar al II-lea termen la ![]() :
:
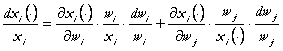 (68)
(68)
Notam " ^ " variatia procentuala
a variabilei, de exemplu ![]() .
.
Putem rescrie (68) ca:
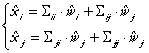 (68')
(68')
Scazand cele doua relatii, obtinem:
![]() (69)
(69)
![]()
Raportam primul si ultimul termen
al sirului de egalitati din (69) la ![]() si obtinem:
si obtinem:
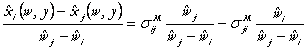 (70)
(70)
cand ![]() .
.
Din (70) rezulta ca ESDD este o combinatie liniara a elasticitatilor Morishima, fiecare din cei doi termeni ai membrului drept reprezinta raspunsul raportului de modificare a doua inputuri la modificarea preturilor lor.
Masoara raspunsul inputurilor relative la modificarea procentuala a preturilor a doi factori, evaluata de-a lungul frontierei preturilor factorilor (locul geometric al combinatiilor de preturi, care mentin costul constant).
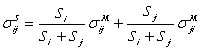 (71)
(71)
unde 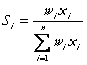 , este ponderea cheltuielilor cu factorul
, este ponderea cheltuielilor cu factorul ![]() in costul total.
in costul total.
EUS este media ponderata a doua elasticitati MORISHIMA, unde ponderile sunt date de cotele parti ale costurilor pentru un factor de productie in costul total.
Presupunem ![]() , de doua ori diferentiabila. Definim, de asemenea o multime
de indici ai preturilor factorilor
, de doua ori diferentiabila. Definim, de asemenea o multime
de indici ai preturilor factorilor ![]() si partitia
si partitia ![]() , unde
, unde ![]() . Definim, de asemenea, multimea extinsa a indicilor
. Definim, de asemenea, multimea extinsa a indicilor ![]() , respectiv
, respectiv ![]() , unde elementul "0" reprezinta indicele outputului.
Corespunzator, partitionam si vectorul preturilor
, unde elementul "0" reprezinta indicele outputului.
Corespunzator, partitionam si vectorul preturilor
![]() .
.
Definim separabilitatea functiei
de cost, in termenii pantei frontierei factorilor. Preturile ![]() si
si ![]() sunt separabile de
sunt separabile de ![]() , in
, in ![]() , daca:
, daca:
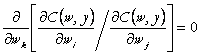 (72)
(72)
Aplicam lema lui Shepard:
![]() (73)
(73)
Derivand (72) in raport cu ![]() , obtinem:
, obtinem:
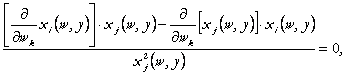
Se obtine imediat ca:
 (74)
(74)
relatie
care inmultita cu ![]() evidentiaza in membrul
din stanga, respectiv din dreapta, elasticitatea incrucisata a cererii derivate
din produsul
evidentiaza in membrul
din stanga, respectiv din dreapta, elasticitatea incrucisata a cererii derivate
din produsul ![]() respectiv
respectiv ![]() , in raport cu pretul factorului
, in raport cu pretul factorului ![]() , adica:
, adica:
![]() (75)
(75)
Separabilitatea functiei de cost
are mai multe implicatii decat separabilitatea functiei de productiei. Rezulta
ca daca ![]() si
si ![]() sunt separabile de
sunt separabile de ![]() , inputurile
, inputurile ![]() si
si ![]() sunt substituibile
Allen, pentru ca elasticitatile incrucisate sunt egale si
sunt substituibile
Allen, pentru ca elasticitatile incrucisate sunt egale si ![]() .
.
Spunem ca functia de cost este slab separabila in partitia ![]() daca:
daca:
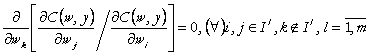 (76)
(76)
Deci functia de cost este slab
separabila, daca panta preturilor factorilor in spatiul ![]() , unde
, unde ![]() si
si ![]() sunt elemente ale
aceleiasi submultimi de preturi in partitia facuta, este independenta de toate
celelalte preturi
sunt elemente ale
aceleiasi submultimi de preturi in partitia facuta, este independenta de toate
celelalte preturi ![]() ale factorilor care nu
sunt elemente din aceasta submultime.
ale factorilor care nu
sunt elemente din aceasta submultime.
Rezulta ca, prin separabilitatea
slabita, elasticitatile cererilor derivate ale tuturor preturilor dintr-o
submultime de factori in raport cu pretul unui input dintr-o alta submultime,
sunt egale (![]() oricare ar fi
oricare ar fi ![]() ). Aceasta proprietate are implicatii econometrice
importante, privind estimarea elasticitatilor cererilor derivate de factori,
numarul acestora fiind considerabil mai redus decat dimensiunea
). Aceasta proprietate are implicatii econometrice
importante, privind estimarea elasticitatilor cererilor derivate de factori,
numarul acestora fiind considerabil mai redus decat dimensiunea ![]() a factorilor, atunci
cand functia de cost este slab separabila.
a factorilor, atunci
cand functia de cost este slab separabila.
In consecinta, o functie de cost slab separabila poate fi specificata prin:
![]() (77)
(77)
unde ![]() este diferentiabila si
monoton crescatoare in raport cu
este diferentiabila si
monoton crescatoare in raport cu ![]() , iar functiile
, iar functiile ![]() respecta proprietatile
functiilor de cost.
respecta proprietatile
functiilor de cost.
Spunem ca functia de cost ![]() este separabila tare in partitia
este separabila tare in partitia ![]() daca:
daca:
 (78)
(78)
si ![]() sau, conform lemei
Shephard:
sau, conform lemei
Shephard:
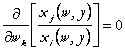 ,
,
adica raportul dintre cererile derivate optimale de factori din oricare doua submultimi disjuncte de inputuri, depinde numai de preturile acestor factori.
Similar cu analiza functiilor de productie, separabilitatea tare implica separabilitatea slaba, dar nu si reciproc.
In cazul separabilitatii tari, functia de cost poate fi reprezentata prin expresia:
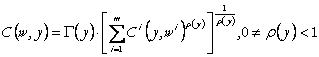 (79)
(79)
sau:
![]() si
si ![]() (79')
(79')
adica
o specificare printr-o functie CES respective Cobb-Douglas, unde termenii ![]() , respecta proprietatile functiilor de cost si
, respecta proprietatile functiilor de cost si ![]() .
.
Separabilitatea tare reflecta
faptul ca in submultimile de factori, conform partitiei facute, toate
inputurile sunt substituibile Allen in aceeasi masura ![]() iar masura Allen este
simetrica.
iar masura Allen este
simetrica.
Cand fiecare submultime de
factori contine un singur input (deci ![]() ) si functia de cost este separabila tare, functia de cost
este separabila in preturi, adica:
) si functia de cost este separabila tare, functia de cost
este separabila in preturi, adica:
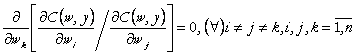 (80)
(80)
si functia de cost poate fi reprezentata prin:
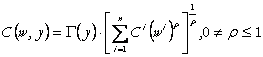 (81)
(81)
sau
![]() (81')
(81')
Datorita dualitatii intre ![]() si
si ![]() se poate demonstra ca
separabilitatea functiei de productie implica separabilitatea functiei de cost
si reciproc.
se poate demonstra ca
separabilitatea functiei de productie implica separabilitatea functiei de cost
si reciproc.
Aplicand metoda staticii comparate, teoremele Euler pentru functii omogene si lema Shepard, deducem cateva proprietati foarte importante, ce pot fi retinute ca legitati de comportament ale functiei de cost in raport cu variatia factorilor determinanti.
Propozitia 1. Functiile cererii derivate de factori sunt omogene de gradul zero in raport cu preturile factorilor; in cosecinta, modificarea simultana cu acelasi indice a preturilor tuturor factorilor (inputurilor) nu modifica cererile derivate din factorii respectivi.
Demonstratie: Consideram o crestere simultana,
cu acelasi indice ![]() a tuturor preturilor.
Functia de cost fiind omogena de grad 1 in preturi, verifica proprietatea:
a tuturor preturilor.
Functia de cost fiind omogena de grad 1 in preturi, verifica proprietatea:
![]() (82)
(82)
adica,
o crestere a preturilor de ![]() ori induce o crestere
a costului de
ori induce o crestere
a costului de ![]() ori. Din lema Shepard,
deducem functiile cererii de inputuri:
ori. Din lema Shepard,
deducem functiile cererii de inputuri:
![]() (83)
(83)
Din (82) obtinem:
![]() (83')
(83')
adica
functiile cererii de factori, ![]() , sunt omogene de grad zero (Q.E.D.).
, sunt omogene de grad zero (Q.E.D.).
In concluzie, functiile cererii derivate de inputuri sunt neutre la cresterea simultana si cu acelasi indice a preturilor pe pietele acestor factori.
Propozitia 2. Intr-o vecinatate a echilibrului la producator, modificarea costului total indusa de modificarea preturilor pe pietele factorilor (inputurilor) este nula.
Demonstratie: Notam
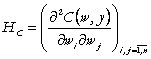 - matricea hessiana
- matricea hessiana
a functiei de cost in raport cu preturile factorilor ![]() .
.
Am vazut mai sus ca functia de cost este omogena de grad 1; aplicam teorema Euler II pentru functii omogene (teorema Euler a hessienei) si obtinem:
![]() (84)
(84)
Din lema Shepard deducem ca
elementele matricei hessiene a functiei de cost comensureaza variatiile
functiilor cererii de factori ![]() induse de modificarile
preturilor acestor factori:
induse de modificarile
preturilor acestor factori:
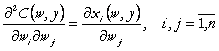 (83'')
(83'')
Conform (84), avem:
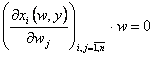 , (84')
, (84')
adica
![]() , (84'')
, (84'')
pentru
fiecare factor ![]() .
.
De exemplu, consideram numai doi
factori (![]() si
si ![]() , capital si munca) avand preturile
, capital si munca) avand preturile ![]() si
si ![]() , modificarile de pret aparute pe cele doua piete vor antrena
modificari ale cererii din acesti factori la producator si in consecinta a
costurilor.
, modificarile de pret aparute pe cele doua piete vor antrena
modificari ale cererii din acesti factori la producator si in consecinta a
costurilor.
Astfel, pentru cererea de forta
de munca (factorul ![]() ), aceste modificari in costuri vor fi nule:
), aceste modificari in costuri vor fi nule:
![]() , (84''.a)
, (84''.a)
si
similar pentru factorul ![]() .
.
Mai mult, insumand aceste modificari pe multimea tuturor factorilor, deducem:
![]() (84''')
(84''')
ceea
ce reflecta continutul proprietatii ![]() .
.
Important este insa ca pentru
determinarea modificarilor in functia de cost generate de variatia preturilor
factorilor, nu este necesara identificarea functiilor cererii induse de
factorii ![]() , intrucat calculul se poate face direct prin (84) folosind
matricea hessiana a functiei de cost. Astfel, modificarile induse in costuri de
variatia preturilor factorilor prin efectele asupra cererii din factorul
, intrucat calculul se poate face direct prin (84) folosind
matricea hessiana a functiei de cost. Astfel, modificarile induse in costuri de
variatia preturilor factorilor prin efectele asupra cererii din factorul ![]() , vor fi cuantificate cu relatia:
, vor fi cuantificate cu relatia:
![]() (84.a)
(84.a)
adica
![]() (84.b)
(84.b)
unde ![]() sunt elementele
matricei hessiene a functiei de cost.
sunt elementele
matricei hessiene a functiei de cost.
Revenind la relatia (84'') sau,
mai sugestiv, la cazul particular (84''.a), cum ![]() trebuie ca variatia
cererii din factorul
trebuie ca variatia
cererii din factorul ![]() in raport cu unele
preturi sa fie negativa si in raport cu altele sa fie pozitiva.
in raport cu unele
preturi sa fie negativa si in raport cu altele sa fie pozitiva.
Propozitia 3. a) Modificarea cererii derivate
din factorul ![]() in raport cu propriul
sau pret este negativa:
in raport cu propriul
sau pret este negativa:
![]() (85)
(85)
b) Modificarea cererii derivate
din factorul ![]() in raport cu pretul
factorului
in raport cu pretul
factorului ![]() este egala cu
modificarea cererii derivate din factorul
este egala cu
modificarea cererii derivate din factorul ![]() in raport cu pretul
factorului
in raport cu pretul
factorului ![]() :
:
![]() (86)
(86)
Demonstratia este imediata si
rezulta din faptul ca matricea hessiana ![]() este negativ definita,
adica:
este negativ definita,
adica:
![]() , unde
, unde ![]() este minorul principal
de ordin
este minorul principal
de ordin ![]() , din matricea
, din matricea ![]() .
.
Cum ![]() rezulta diagonala
principala a matricei
rezulta diagonala
principala a matricei ![]() este negativa si
conform (83'') deducem
este negativa si
conform (83'') deducem ![]() .
.
Proprietatea b) rezulta din aceea
ca ![]() este simetrica .
este simetrica .
Trebuie sa observam ca cele doua
componente ale proprietatii ![]() au fost deja
evidentiate cu ajutorul teoremei lui Slutsky aplicata la producator:
au fost deja
evidentiate cu ajutorul teoremei lui Slutsky aplicata la producator:
- variatia reziduala a factorului
![]() indusa de modificarea
cu o unitate a pretului sau este negativa:
indusa de modificarea
cu o unitate a pretului sau este negativa: ![]()
- variatia reziduala a factorului
![]() indusa de modificarea
cu
indusa de modificarea
cu
o unitate a pretului factorului ![]() este egala cu variatia
reziduala
este egala cu variatia
reziduala
a factorului ![]() indusa de modificarea
cu o unitate a pretului
indusa de modificarea
cu o unitate a pretului
factorului ![]() .
.
Propozitia 4. Suma elasticitatilor cererii
derivate de factor ![]() in raport cu preturile
tuturor inputurilor
in raport cu preturile
tuturor inputurilor ![]() este nula.
este nula.
![]() , unde
, unde ![]() (87)
(87)
Demonstratia se fundamenteaza pe
proprietatea ![]() , impartind relatia (84'') la
, impartind relatia (84'') la ![]() (unde
(unde ![]() ).
).
In consecinta, elasticitatea la
scala de fabricatie ![]() a utilizarii
factorului
a utilizarii
factorului ![]() este nula, deci
tehnologia evidentiaza caracteristica de venituri strict descrescatoare la
scala de fabricatie.
este nula, deci
tehnologia evidentiaza caracteristica de venituri strict descrescatoare la
scala de fabricatie.
Din relatia (87) deducem in plus ca:
- ![]() (87')
(87')
Cum elasticitatea cererii din
factorul ![]() in raport cu propriul
pret este negativa
in raport cu propriul
pret este negativa ![]() , conform (85) rezulta ca suma elasticitatilor incrucisate cerere-pret
este pozitiva si (87') reflecta proprietatea ca suma cresterilor procentuale a
cererii din factorul
, conform (85) rezulta ca suma elasticitatilor incrucisate cerere-pret
este pozitiva si (87') reflecta proprietatea ca suma cresterilor procentuale a
cererii din factorul ![]() pe seama cresterii cu
1% a preturilor celorlalti factori, egaleaza valoarea absoluta a descresterii
(%) cererii din acest input indusa de cresterea cu 1% a propriului pret.
pe seama cresterii cu
1% a preturilor celorlalti factori, egaleaza valoarea absoluta a descresterii
(%) cererii din acest input indusa de cresterea cu 1% a propriului pret.
Trebuie observat ca, chiar daca
variatiile marginale ale cererilor din doi factori ![]() si
si ![]() pe seama pretului
celuilalt factor sunt egale, conform Propozitiei
3 formula (85), elasticitatile corespunzatoare sunt diferite, adica
pe seama pretului
celuilalt factor sunt egale, conform Propozitiei
3 formula (85), elasticitatile corespunzatoare sunt diferite, adica
![]() (86')
(86')
Aceasta arata ca o crestere cu 1%
a pretului ![]() respectiv
respectiv ![]() , induce o crestere (%) a cererii din cei doi factori
diferita, proprietate ce decurge din nivelul diferit de utilizare a celor doua
inputuri.
, induce o crestere (%) a cererii din cei doi factori
diferita, proprietate ce decurge din nivelul diferit de utilizare a celor doua
inputuri.
Analizam efectele induse de modificarea outputului asupra functiilor de cost: costul marginal, costul total, etc.
Fie ![]() functia de cost
(total). Atunci costul marginal este
functia de cost
(total). Atunci costul marginal este ![]() .
.
Din proprietatea ca functia de cost este nedescrescatoare in raport cu volumul outputului, rezulta ca functia costului marginal este nenegativa.
Deoarece functia de cost este omogena de grad 1, din (82) se deduce ca functia costului marginal are aceeasi proprietate:
![]() (82')
(82')
Propozitia 5. Variatia cererii derivate din
inputul ![]() la o crestere de o
unitate a outputului
la o crestere de o
unitate a outputului ![]() este egala cu variatia
costului marginal in raport cu cresterea cu o unitate a pretului inputului
este egala cu variatia
costului marginal in raport cu cresterea cu o unitate a pretului inputului ![]() :
:
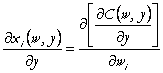 (88)
(88)
Demonstratia se bazeaza pe lema
Shepard si se deduce imediat din relatia (83) derivand in raport cu ![]() .
.
Dupa sensul variatiei cererii
derivate din factorul ![]() la cresterea
productiei
la cresterea
productiei ![]() se evidentiaza doua
situatii:
se evidentiaza doua
situatii:
- daca ![]() , factorul
, factorul ![]() este un input normal
este un input normal
- in caz contrar, factorul ![]() este un input inferior
este un input inferior
Este evident ca un producator nu poate opera achizitionand numai factori inferiori.
Propozitia 6. Variatia procentuala a costului
total in raport cu modificarea procentuala a nivelului outputului ![]() este inversa
elasticitatii scalei de fabricatie.
este inversa
elasticitatii scalei de fabricatie.
Masuram variatia procentuala a costului total in raport cu variatia (%) a outputului, prin indicatorul flexibilitatea costului:
![]() (89)
(89)
adica
pentru functia de cost ![]() care este
diferentiabila avem:
care este
diferentiabila avem:
![]() (89')
(89')
relatie
care arata pe de o parte ca acest indicator este o elasticitate (elasticitatea
costului total in raport cu outputul) si pe de alta, ca ![]() este raportul intre
costul marginal si cel mediu.
este raportul intre
costul marginal si cel mediu.
Asadar Popozitia 6 se poate enunta si astfel:
Propozitia 6'. Elasticitatea costului in raport cu outputul este egala cu inversa elasticitatii scalei de fabricatie:
![]() (90)
(90)
Demonstratie: Pornim de la problema de fundamentare a
deciziei optime prin minimizarea costurilor, la nivelul productiei
![]()
![]() .
.
si
(91)
![]() este functia de productie
este functia de productie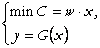
Scriind lagrangeanul, deducem conditiile necesare de optim:
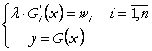 (91')
(91')
Inmultim prima ecuatie din (91')
cu ![]() si insumam:
si insumam:
![]() (92)
(92)
unde,
dupa cum se stie, multiplicatorul Lagrange ![]() are interpretarea:
are interpretarea:
![]() (93)
(93)
unde ![]() este nivelul optim (minim)
al costului in problema (91).
este nivelul optim (minim)
al costului in problema (91).
Membrul drept din (92) se poate scrie:
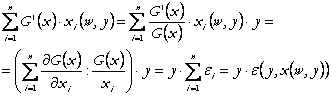 (94)
(94)
unde ![]() este elasticitatea
scalei de fabricatie calculata ca suma a elasticitatilor productiei in raport
cu factorii utilizati si este dependenta de volumul factorilor utilizati
este elasticitatea
scalei de fabricatie calculata ca suma a elasticitatilor productiei in raport
cu factorii utilizati si este dependenta de volumul factorilor utilizati ![]() si de volumul
outputului
si de volumul
outputului ![]() .
.
Din (92) si (94) deducem:
![]() (92')
(92')
In (92') membrul din stanga
defineste functia de cost ![]() . Tinand cont si de (93) rezulta:
. Tinand cont si de (93) rezulta:
![]()

Consecinta: ![]()
adica: in conditiile deciziei optime de
minimizare a costurilor firma isi desfasoara activitatea in conditii de
venituri crescatoare la scala de fabricatie ![]() , daca si numai daca inregistreaza venituri descrescatoare la
elasticitatea cost/productie
, daca si numai daca inregistreaza venituri descrescatoare la
elasticitatea cost/productie ![]() si invers.
si invers.
Chiar daca cele doua concepte sunt relativ apropiate, trebuie subliniat ca elasticitatea scalei de fabricatie masoara raspunsul (reactia) outpututlui de-a lungul razei (dreptei) scalei de fabricatie in spatiul inputurilor, in timp ce elasticitatea cost/output (cost/productie) comensureaza raspunsul outputului de-a lungul traiectoriei de dezvoltare a firmei in spatiul inputurilor (adica locul geometric al punctelor din acest spatiu in care costul de fabricatie este minim).
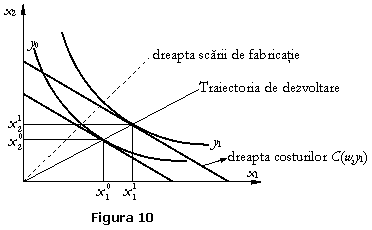
Cele doua masuri corespund
aceleiasi combinatii de inputuri daca si numai daca dreapta scalei de
fabricatie este suprapusa peste traiectoria de dezvoltare a firmei. Astfel, in
spatiul inputurilor ![]() putem ilustra aceste concepte
ca in figura 10.
putem ilustra aceste concepte
ca in figura 10.
Observatii: Flexibilitatea costului, ca si
elasticitatea scalei de fabricatie, sunt indicatori folositi in decizia de
dezvoltare a firmei. Presupunem ca, la un pret al pietei outputului, fixat,
firma are posibilitatea de a produce o cantitate ![]() intr-un singur proces
sau sa produca volumul
intr-un singur proces
sau sa produca volumul ![]() in fiecare din
in fiecare din ![]() procese de productie.
procese de productie.
Daca ![]() , este mai avantajos sa produca in
, este mai avantajos sa produca in ![]() procese intrucat agregarea productiei in cele
procese intrucat agregarea productiei in cele ![]() procese va conduce la pierderi prin cresterea productiei
(conform consecintei de mai sus). In caz contrar, este mai avantajos sa produca
intregul output
procese va conduce la pierderi prin cresterea productiei
(conform consecintei de mai sus). In caz contrar, este mai avantajos sa produca
intregul output ![]() intr-un singur proces,
intrucat firma va inregistra economii (venituri crescatoare la scala de
fabricatie).
intr-un singur proces,
intrucat firma va inregistra economii (venituri crescatoare la scala de
fabricatie).
In cazul ![]() , este indiferent ce decizie va lua: de a produce in
, este indiferent ce decizie va lua: de a produce in ![]() procese sau intr-un singur proces, intrucat nu se
inregistreaza nici pierderi nici venituri intr-o situatie decizionala sau alta.
procese sau intr-un singur proces, intrucat nu se
inregistreaza nici pierderi nici venituri intr-o situatie decizionala sau alta.
Problema a fost studiata de Uzawa (1963), Shephard (1970), Friedman (1972), McFadden (1978) si dezvoltata ulterior intr-o diversitate de studii de numerosi cercetatori, din diferite tari.
Conform teoremei Minkowski, orice
multime inchisa si convexa in ![]() este intersectia
semispatiilor de sustinere, unde prin definitie, orice subspatiu in
este intersectia
semispatiilor de sustinere, unde prin definitie, orice subspatiu in ![]() este reprezentat prin:
este reprezentat prin:
![]() (95)
(95)
Observam deci ca functia de cost
defineste in spatiul inputurilor un semispatiu, pentru orice vector de preturi ![]() si orice nivel fixat
si orice nivel fixat ![]() al outputului:
al outputului:
![]() (95')
(95')
unde ![]() este costul minim al
productiei
este costul minim al
productiei ![]() .
.
Ca o consecinta, constatam ca nu
exista un vector de inputuri ![]() care sa permita
realizarea productiei
care sa permita
realizarea productiei ![]() cu un cost mai mic,
adica
cu un cost mai mic,
adica ![]() .
.
Rezulta ca acea combinatie de
inputuri ![]() , care minimizeaza costul pentru preturile
, care minimizeaza costul pentru preturile ![]() fixate de piata si
fixate de piata si ![]() dat, este situata pe
frontiera semispatiului
dat, este situata pe
frontiera semispatiului ![]() si este data de
hiperplanul
si este data de
hiperplanul ![]() .
.
Notam:
![]()
si
![]()
unde ![]() este functia de
productie a firmei cu tehnologia existenta. Deci
este functia de
productie a firmei cu tehnologia existenta. Deci ![]() defineste multimea
inputurilor necesare pentru realizarea productiei
defineste multimea
inputurilor necesare pentru realizarea productiei ![]() , cu tehnologia data.
, cu tehnologia data.
Teorema dualitatii cost-productie
ilustreaza proprietatea ca, in conditiile tehnologice date, ![]() .
.
Consideram, pentru simplificare,
multimea preturilor inputurilor care conduc la un cost unitar, pentru un anumit
nivel al outputului ![]() - numita curba izocost unitara.
- numita curba izocost unitara.
Fie ![]() - regiunea din
- regiunea din ![]() in care nivelul productiei
in care nivelul productiei
![]() se obtine cu un cost
supraunitar.
se obtine cu un cost
supraunitar.
Deoarece ![]() este convexa in
spatiul
este convexa in
spatiul ![]() , multimea
, multimea ![]() este concava. Multimea
este concava. Multimea
![]() se numeste multimea
preturilor factorilor necesari realizarii outputului
se numeste multimea
preturilor factorilor necesari realizarii outputului ![]() si se pune in
corespondenta cu multimea
si se pune in
corespondenta cu multimea ![]() , cu deosebirea ca
, cu deosebirea ca ![]() este multimea de
inputuri pe cand
este multimea de
inputuri pe cand ![]() este multimea
preturilor acestora.
este multimea
preturilor acestora.
![]() este frontiera
preturilor factorilor, numita, asa cum am mentionat, curba izocost unitara. Ce
relatie exista intre modificarile a doua preturi cu
este frontiera
preturilor factorilor, numita, asa cum am mentionat, curba izocost unitara. Ce
relatie exista intre modificarile a doua preturi cu ![]() si dwj de-a lungul acestei
curbe?
si dwj de-a lungul acestei
curbe?
Diferentiind ![]() pentru
pentru ![]() dat, obtinem:
dat, obtinem:
![]()
in
care, consideram ca ![]() . Deducem ca imediat, folosind lema lui Shepard:
. Deducem ca imediat, folosind lema lui Shepard:
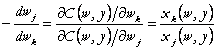 (96)
(96)
expresie
care comensureaza panta frontierei preturilor factorilor in planul ![]() , panta care este negativa.
, panta care este negativa.
Astfel, daca pretul inputului ![]() creste cu o unitate,
pentru a se mentine pe curba izocost unitara, firma trebuie sa utilizeze acel
factor
creste cu o unitate,
pentru a se mentine pe curba izocost unitara, firma trebuie sa utilizeze acel
factor ![]() , al carui pret scade cu o marime egala cu raportul intre
cantitatile optime ce trebuie utilizate din cei doi factori
, al carui pret scade cu o marime egala cu raportul intre
cantitatile optime ce trebuie utilizate din cei doi factori ![]() .
.
Dar din CNO ale problemei de
minimizare a costurilor in conditiile functiei de productiei ![]() , stim ca:
, stim ca:
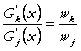 (97)
(97)
Insa de-a lungul izocuantei ![]() , stim de asemenea ca RMS (rata marginala de substitutie)
este
, stim de asemenea ca RMS (rata marginala de substitutie)
este
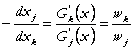 , (98)
, (98)
relatia care exprima panta izocuantei in functie de preturile factorilor, pe cand (96) exprima panta curbei de izocost in functie de inputuri.
In concluzie, relatiile (96) si (98) reflecta dualitatea cost-productie.
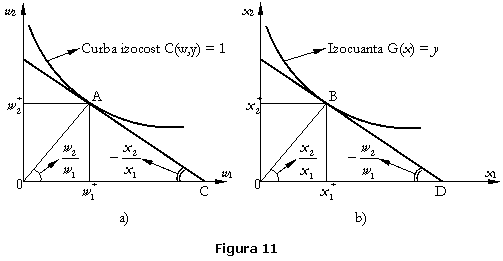
Pentru ilustrare, consideram doi
factori ![]() si facem reprezentarea
in spatiul preturilor. Panta curbei izocost este
si facem reprezentarea
in spatiul preturilor. Panta curbei izocost este ![]() , frontiera preturilor factorilor este
, frontiera preturilor factorilor este ![]() , care are aceeasi panta
, care are aceeasi panta ![]() (vezi fig. ..,a),
punctul de tangenta fiind A. Raza (dreapta) OA are panta egala cu
(vezi fig. ..,a),
punctul de tangenta fiind A. Raza (dreapta) OA are panta egala cu ![]() si conform (98)
aceasta este egala cu RMS. Asadar, din frontiera preturilor factorilor se poate
obtine atat panta izocuantei
si conform (98)
aceasta este egala cu RMS. Asadar, din frontiera preturilor factorilor se poate
obtine atat panta izocuantei 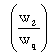 cat si nivelul relativ
de utilizare a factorilor
cat si nivelul relativ
de utilizare a factorilor ![]() .
.
Similar, reprezentarea in spatiul
factorilor (fig. 11.b) evidentiaza ca raza OB are panta ![]() unde B este punctul de
tangenta al izocuantei la linia costurilor, panta izocuantei fiind
unde B este punctul de
tangenta al izocuantei la linia costurilor, panta izocuantei fiind ![]() . Deci cunoasterea izocuantei permite determinarea atat a
pantei frontierei preturilor factorilor cat si nivelul relativ al preturilor.
. Deci cunoasterea izocuantei permite determinarea atat a
pantei frontierei preturilor factorilor cat si nivelul relativ al preturilor.
Geometric, dualitatea intre
functia de cost si functia de productie reflecta congruenta triunghiurilor OAC
si OBD in reprezentarea in spatiul preturilor respectiv al factorilor, unghiul ![]() fiind egal cu unghiul
fiind egal cu unghiul ![]() si
si ![]() .
.
Ilustram rezultatele teoretice
anterioare, in cazul concret in care functia de productie este de tip
Cobb-Douglas cu doi factori: ![]() :
:
![]()
Presupunem ca firma analizata
activeaza pe o piata care are capacitate de absorbtie suficient de mare din
outputul ![]() al firmei. In aceste
conditii, modelul de optimizare are ca obiectiv maximizarea productiei
al firmei. In aceste
conditii, modelul de optimizare are ca obiectiv maximizarea productiei ![]() in conditiile in care
costul este fixat,
in conditiile in care
costul este fixat, ![]() , unde
, unde
![]()
preturile
celor doi factori fiind ![]() (salariul nominal
mediu pe persoana, pe an, platit de firma) si
(salariul nominal
mediu pe persoana, pe an, platit de firma) si ![]() - costul capitalului
(lei/1 miliard lei capital tehnic),
- costul capitalului
(lei/1 miliard lei capital tehnic), ![]() - costul fix -
exclusiv amortizarile.
- costul fix -
exclusiv amortizarile.
Vom deduce functia de cost ![]() . Scriind lagrangeanul si aplicand conditiile necesare de
optim obtinem:
. Scriind lagrangeanul si aplicand conditiile necesare de
optim obtinem:
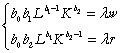 (99)
(99)
unde ![]() este multiplicatorul
Lagrange,
este multiplicatorul
Lagrange, ![]() ,
, ![]() fiind productia
optima.
fiind productia
optima.
Impartind cele doua CNO deducem
nivelul relativ al cererii de factori ![]() reprezentand nivelul
optim al dotarii tehnice la acesta firma in functie de nivelul relativ al
preturilor
reprezentand nivelul
optim al dotarii tehnice la acesta firma in functie de nivelul relativ al
preturilor ![]() :
:
![]() , (99')
, (99')
deci necesarul de munca in raport cu volumul capitalului este
![]()
Inlocuind in functia de
productie, deducem necesarul ![]() de capital in functie
de nivelul dorit al productiei:
de capital in functie
de nivelul dorit al productiei:
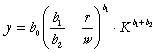
deci:
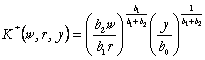 (100)
(100)
In consecinta necesarul de forta de munca va fi:
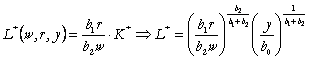 (101)
(101)
Inlocuind in ecuatia costului, deducem functia de cost:
![]()
si dupa efectuarea calculelor, gasim:
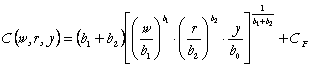 (102)
(102)
Asadar, dupa cum am demonstrat teoretic cunoscand functia de productie, putem deduce functia de cost.
Se verifica prin calcul direct valabilitatea lemei Shepard
![]() si
si ![]()
(propunem ca exercitii efectuarea calculelor)
Asadar
![]() (102.A)
(102.A)
si prin calcul direct, regasim
![]() (102'.A)
(102'.A)
care defineste panta frontierei preturilor, negativa si proportionala cu raportul preturilor, de-a lungul curbei izocostului unitar.
Din (101) deducem ca de-a lungul
izocuantei ![]() - fixat, avem RMS:
- fixat, avem RMS:
![]() (101.A)
(101.A)
care defineste panta izocuantei. Din (99'.A) si (101.A) deducem ca intre pantele celor doua curbe (curba izocost si curba izocuanta) exista relatia:
![]() (102'.A)
(102'.A)
care evidentiaza rolul elasticitatilor productiei in raport cu factorii in determinarea raportului intre cele doua pante.
Ilustram acum si a doua componenta a teoremei dualitatii: cunoscand functia de cost, putem identifica functia de productie.
Intr-adevar, cunoscand functia de
cost (102), prin aplicarea lemei Shepard determinam cererea de factori ![]() , avand expresiile (100), (101) si de-a lungul curbei izocost
deducem (102.A). Folosind relatia (102'.A) in care inlocuim panta
, avand expresiile (100), (101) si de-a lungul curbei izocost
deducem (102.A). Folosind relatia (102'.A) in care inlocuim panta ![]() cu (102.A), gasim:
cu (102.A), gasim:
![]() (102''.A)
(102''.A)
care
se poate scrie: ![]()
Prin integrare deducem:
![]() constanta
constanta
deci izocuanta:
![]() , adica expresia functiei de productie
, adica expresia functiei de productie 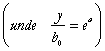 de la care am pornit.
de la care am pornit.
Studii de caz propuse: reluati analiza de mai sus daca functia de productie este de tip CES:
a)
![]()
b)
![]() , a > 0, b > 0.
, a > 0, b > 0.
Vom corecta efectele induse de diferite socuri asupra cererii de factori, deci asupra outputului.
Pornim de la modelul deciziei optime:
![]() (1)
(1)
unde:
- ![]() este vectorul
preturilor;
este vectorul
preturilor;
- 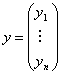 este vectorul de
productie,
este vectorul de
productie,
cu ![]()
![]()
-![]() este functia de productie, respectiv restrictia tehnologica,
definita pe frontiera eficienta.
este functia de productie, respectiv restrictia tehnologica,
definita pe frontiera eficienta.
Consideram functia de productie
monooutput ![]() , considerand
, considerand ![]() factori de productie.
factori de productie.
Putem formula pentru ![]() fixata problema (1),
ca o problema de minimizare a costurilor pentru atingerea unui nivel determinat
al productiei finite,
fixata problema (1),
ca o problema de minimizare a costurilor pentru atingerea unui nivel determinat
al productiei finite, ![]() .
.
 (2)
(2)
Rezolvam problema (2) prin metoda
multiplicatorilor Lagrange, obtinand ![]() valoarea optima a
functiei obiectiv pentru
valoarea optima a
functiei obiectiv pentru ![]() fixat.
fixat.
Problema duala a problemei (1)
este o problema de maximizare a productiei in conditiile incadrarii in nivelul ![]() de cheltuieli de
productie.
de cheltuieli de
productie.
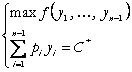 (3)
(3)
Functia Lagrange, atasata problemei (1) este:
![]() (4)
(4)
Presupunem ca firma functioneaza in competitie perfecta, astfel incat preturile pe pietele factorilor si de productie finite sunt fixate.
Conditia necesara de optim atasata problemei (3) este:
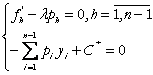 (5)
(5)
unde: ![]()
Diferentiem conditia de ordinul
intai in raport cu ![]() si
si ![]() , obtinem sistemul de ecuatii Slutsky:
, obtinem sistemul de ecuatii Slutsky:
 (6)
(6)
Urmarim sa determinam variatia
cererilor derivate (de factori de productie), indusa de variatia cheltuielilor
de productie ![]() si a preturilor pe
pietele factorilor.
si a preturilor pe
pietele factorilor.
Ipoteza 1
![]() .
.
Rezolvam (6) prin metoda lui Cramer.
Construim matricea Hessian bordata:
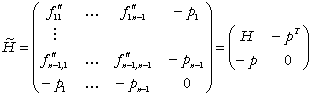 (7)
(7)
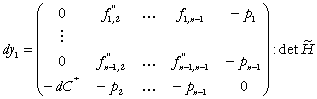 (8)
(8)
![]() (9)
(9)
unde ![]() este cofactorul
(minorul cu semn corespunzator elementului
este cofactorul
(minorul cu semn corespunzator elementului ![]() din
din ![]() ) si H este matricea hessiana a functiei de productie, H I Mn - 1,n - 1.
) si H este matricea hessiana a functiei de productie, H I Mn - 1,n - 1.
Raportul:
![]() (10)
(10)
este variatia compensata a cheltuielilor, efect de cheltuieli sau efect de output.
In general, pentru orice ![]() , obtinem:
, obtinem:
![]() (11)
(11)
adica
variatia compensata de cheltuieli indusa de modificarea cu o unitate monetara a
cheltuielilor totale ale firmei ![]() , asupra cererii derivate din factorul de productie
, asupra cererii derivate din factorul de productie ![]() .
.
Ipoteza 2
![]() .
.
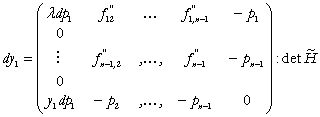 (12)
(12)
Rezolvam (12) dezvoltand dupa prima coloana:
![]() (13)
(13)
Rescriem (13) tinand cont de 10:
![]() (14)
(14)
Generalizand (14), obtinem:
![]() (15)
(15)
In (15), primul termen reflecta
efectul de substitutie indus de modificarea pretului ![]() , asupra cererii derivate de factor
, asupra cererii derivate de factor ![]() , iar al doilea termen reprezinta variatia compensata de
cheltuieli. Suma acestor doi termeni, coeficientul Slutsky, reflecta variatia
reziduala prin efectul de substitutie si de variatie compensata de cheltuieli,
indusa de modificarea cu o unitate monetara a pretului produsului
, iar al doilea termen reprezinta variatia compensata de
cheltuieli. Suma acestor doi termeni, coeficientul Slutsky, reflecta variatia
reziduala prin efectul de substitutie si de variatie compensata de cheltuieli,
indusa de modificarea cu o unitate monetara a pretului produsului ![]() asupra cererii
derivate de factor
asupra cererii
derivate de factor ![]() .
.
Notam simbolic efectul de
substituire 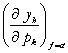 (primul termen din
(15)) si efectul de cheltuieli
(primul termen din
(15)) si efectul de cheltuieli  al doilea termen din
(15), iar coeficientul Slutsky
al doilea termen din
(15), iar coeficientul Slutsky ![]() .
.
In conformitate cu teorema lui Slutsky deducem:
(1) ![]() variatia reziduala a
modificarii cu o unitate a pretului
variatia reziduala a
modificarii cu o unitate a pretului ![]() , asupra cererii derivatei de factori
, asupra cererii derivatei de factori ![]() , prin efectul de substituire si variatia compensata de
cheltuieli, este egala cu variatia reziduala a modificarii pretului
, prin efectul de substituire si variatia compensata de
cheltuieli, este egala cu variatia reziduala a modificarii pretului ![]() asupra cererii
derivate de factori
asupra cererii
derivate de factori ![]() prin efectul de
substituire si variatia compensata de cheltuieli.
prin efectul de
substituire si variatia compensata de cheltuieli.
(2) 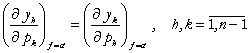 : efectele de substituire sunt egale (in realitate,
substitutia perfecta nu se poate realiza).
: efectele de substituire sunt egale (in realitate,
substitutia perfecta nu se poate realiza).
(3) 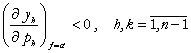 : in conditiile normale ale cererii si ofertei, efectele de
substituire sunt negative, respectiv o scadere a pretului va indica o crestere
a cererii.
: in conditiile normale ale cererii si ofertei, efectele de
substituire sunt negative, respectiv o scadere a pretului va indica o crestere
a cererii.
(4) In conditiile normale ale
cererii si ofertei, matricea Slutsky K
este negativ definita (minorii principali au semnul ![]() , unde
, unde ![]() este ordinul
minorului) si simetrica.
este ordinul
minorului) si simetrica.
(5) ![]()
Deoarece K este negativ definita, rezulta:
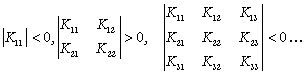
Respectiv:

Aplicatie:
Analiza sensitivitatii cererilor derivate de factori la modificarile cheltuielilor totale ale firmei si la modificarea preturilor factorilor.
Consideram o tehnologie formalizata cu ajutorul unei functii de productie neoclasice monoproduct cu factori substituibili, pe frontiera eficienta (analiza fiind valabila pentru functiile de productie multiproduct).
![]()
unde Y este outputul firmei, iar ![]() sunt inputurile
firmei.
sunt inputurile
firmei.
Pentru un nivel de output fixat ![]() , problema de maximizare a profitului devine problema de
minimizare a costurilor:
, problema de maximizare a profitului devine problema de
minimizare a costurilor:
 (1)
(1)
Solutionarea problemei (1) prin
metoda multiplicatorilor Lagrange va conduce la functiile de cerere derivata
ale firmei ![]() si
si ![]() , valoarea functiei obiectiv, respectiv costul total minim.
, valoarea functiei obiectiv, respectiv costul total minim.
Duala problemei (1) este:
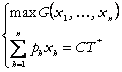 (2)
(2)
care, solutionata prin metoda multiplicatorilor Lagrange, va conduce la functiile de cerere derivata.
Pe baza conditiilor de optim de ordinul al II-lea ale problemei (2), dorim sa determinam modificarea cererii derivate de factori in raport cu modificarile preturilor, pe de o parte, cat si cu modificarile obiectivelor totale pe care firma este dispusa sa le afecteze productiei. Pentru aceasta vom folosi un rezultat fundamental (in teoria microeconomica si anume acela oferit de economistul american Eugen Slutsky, concretizat in teoria lui Slutsky prezentata in cursul de Cibernetica economica partea a II-a.
Aplicatie numerica:
Consideram functia de productie cu factori substituibili pe termen scurt:
![]()
unde:
- ![]() este factorul capital
circulant in unitati fizice;
este factorul capital
circulant in unitati fizice;
-![]() este factorul munca in unitati fizice (an - ore).
este factorul munca in unitati fizice (an - ore).
ambii factori fiind variabili pe termen scurt, iar
-![]() este volumul outputului.
este volumul outputului.
Consideram ![]() unitati fizice,
volumul fixat al outputului. Notam
unitati fizice,
volumul fixat al outputului. Notam ![]() pretul pietei pentru
factorul capital circulant si
pretul pietei pentru
factorul capital circulant si ![]() pretul pietei pentru
factorul munca.
pretul pietei pentru
factorul munca.
Consideram ca in perioada
precedenta preturile pietei au fost ![]() si
si ![]() .
.
Cu datele considerate problema de minimizare a costurilor pentru atingerea unui nivel fixat al productiei, devine:
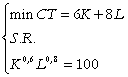 (3)
(3)
CNO
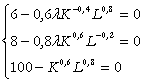 (4)
(4)
Raportand prima ecuatie la a doua:
![]()
Inlocuim rezultatul de mai sus in a treia ecuatie din sistemul (4):
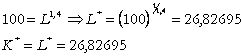 (5)
(5)
Din prima ecuatie avem si ![]() ,
, 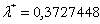 .
.
Duala problemei de minimizare a costurilor pentru atingerea unui nivel fixat al productiei fizice este:
CNO
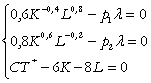 (6)
(6)
Diferentiem conditia necesara de optim:
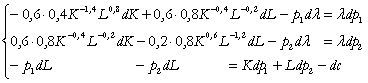 (7)
(7)
Stiind ca optimul initial ![]() , iar
, iar ![]() rescriem relatiile de
mai sus tinand cont de aceste rezultate:
rescriem relatiile de
mai sus tinand cont de aceste rezultate:
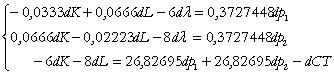 (8)
(8)
Sistemul rezultat este un sistem
algebric liniar, pe care il rezolvam in ![]() si
si ![]() .
.
Matricea sistemului este Hessiana bordata, pe care am folosit-o pentru formularea conditiei de ordinul doi a problemei de decizie optimala la producator:
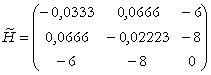
I. Dorim sa identificam efectul modificarii cheltuielilor totale ale firmei asupra cererii derivate de factori. Pentru aceasta facem ipotezele:
![]()
Rezolvarea prin regula lui Crammer ne conduce la rezultatele:
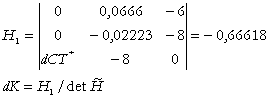
Dezvoltand dupa prima coloana:

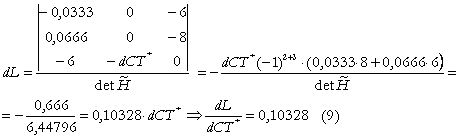
Relatiile (8) si (9) reprezinta efectul de cheltuieli, (variatia compensata de cheltuieli), adica modificarea cererii derivate de factor K, respectiv L, indusa de modificarea cu o unitate monetara a cheltuielilor.
II. Dorim sa identificam efectul modificarii preturilor pietei pentru cei doi factori, asupra cererii derivate de factori.
(IIa) ![]()
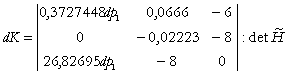 (10)
(10)
Din (10) deducem:
 (11)
(11)
este efectul total de substitutie si de cheltuieli al cererii de factor K, indus de modificarea propriului pret.
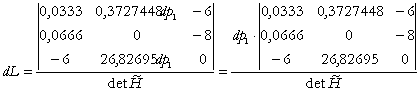 (12)
(12)
Þ ![]() (13)
(13)
este efectul total de substitutie si de cheltuieli al cererii de factor L, indus de modificarea pretului p1, al capitalului.
(IIb) ![]()
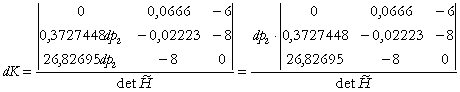 (14)
(14)
Þ ![]() (15)
(15)
este efectul total de substitutie si de cheltuieli al cererii de factor K, indus de modificarea pretului p2, al muncii.
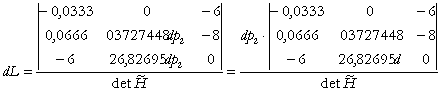 (16)
(16)
Þ ![]() (17)
(17)
este efectul total de substitutie si de cheltuieli al cererii de munca indus de modificarea propriului pret
Ecuatiile (11), (13), (15), (17) sunt ecuatiile Slutsky, in care primii termeni reprezinta efectul de substituire, iar al II-lea termen reprezinta efectul de cheltuieli.
Matricea Slutsky este:
![]()
![]() , elementele matricii Slutsky, reprezinta variatia reziduala
a consumului de factor, prin efectul de substituire si variatia compensata
, elementele matricii Slutsky, reprezinta variatia reziduala
a consumului de factor, prin efectul de substituire si variatia compensata
de cheltuieli indusa de modificarea cu o unitate monetara a pretului produsului
j.
(a) Coeficientii Slutsky simetrici fata de diagonala principala sunt egali:
(b)
![]() (variatiile reziduale
sunt egale)
(variatiile reziduale
sunt egale)
(c) Efectele de substituire ale modificarii pretului unui produs asupra propriului produs sunt intotdeauna negative:
(d)
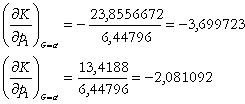
Modificarea
pretului unui factor va determina modificarea, in sens contrar a cantitatii de
factor folosita. De exemplu, daca pretul factorului ![]() scade cu o unitate
monetara, consumul de factor
scade cu o unitate
monetara, consumul de factor ![]() va creste cu 3,69723
unitati fizice.
va creste cu 3,69723
unitati fizice.
(c) Daca sunt satisfacute legile normale ale cererii si ofertei, matricea Slutsky este negativ definita.
![]()
III. Sa se reprezinte grafic punctul de optim initial.
a Curba de indiferenta
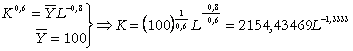
care este ecuatia unei hiperbole echilatere in cadranele 1 si 3.
b) Dreapta isocost
![]()
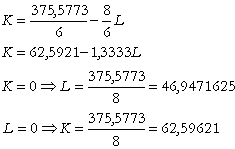
Pretul de optim se situeaza in punctul de tangenta al isocuantei cu dreapta isocost.
c) Conditia de tangenta:

Determinam ![]() din dreapta isocost:
din dreapta isocost:
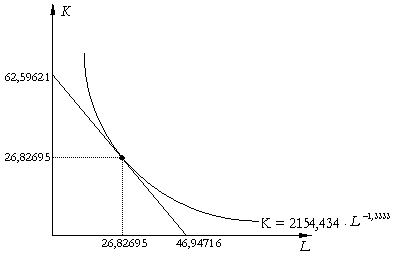
![]()
IV. Presupunem ca pretul
factorului ![]() scade cu doua unitati
monetare.
scade cu doua unitati
monetare.
i) Sa se determine efectul de substituire si sa se reprezinte grafic noua curba isocost.

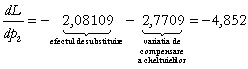
La
scaderea cu o unitate a pretului ![]() , consumul de factor
, consumul de factor ![]() scade cu 2,77479
unitati
scade cu 2,77479
unitati
La
scaderea cu o unitate monetara a pretului ![]() , consumul de factor
, consumul de factor ![]() creste cu 2,08109
unitati
creste cu 2,08109
unitati
Atunci cand ![]() scade cu doua unitati,
noul
scade cu doua unitati,
noul ![]() este:
este:
![]() unitati
unitati
Atunci cand ![]() scade cu doua unitati,
noul
scade cu doua unitati,
noul ![]() este:
este:
![]() unitati
unitati
Cheltuielile totale:
![]() lei
lei
Noua curba izocost:
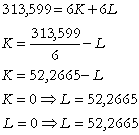
Prin efectul de substituire, s-a
inlocuit ![]() prin
prin ![]() dar productia a ramas
constanta (deci isocuanta din aplicatia de indiferenta se pastreaza).
dar productia a ramas
constanta (deci isocuanta din aplicatia de indiferenta se pastreaza).
Conditia de tangenta
![]()
![]()
![]()
![]()
![]()
![]()
![]()
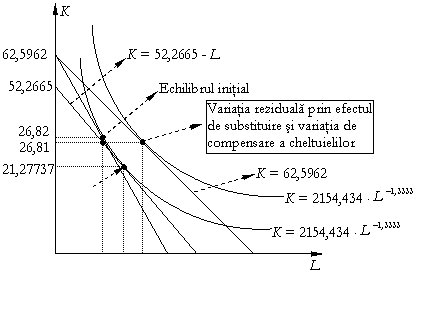
ii) Sa se determine
variatia reziduala prin efectul de stustituire si variatia compensata de
cheltuieli.
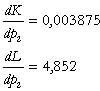
Daca ![]() scade cu o unitate monetara,
scade cu o unitate monetara, ![]() scade cu 0,003875.
scade cu 0,003875.
Daca ![]() creste cu o unitate,
creste cu o unitate, ![]() creste cu 4,852
unitati.
creste cu 4,852
unitati.
Prin efectul de substituire si
variatia de compensare a cheltuielilor indusa de scaderea cu doua unitati a
pretului ![]() , noile valori optimale ale cererilor derivate sunt:
, noile valori optimale ale cererilor derivate sunt:
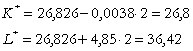
Cheltuielile totale:
![]()
Valoarea productiei pentru noile valori de echilibru:
![]()
Valoarea productiei a crescut
fata de ![]() la
la ![]() in conditiile
mentinerii cheltuielilor de productie constante.
in conditiile
mentinerii cheltuielilor de productie constante.
Ecuatia isocuantei:
![]()
Curba isocost:
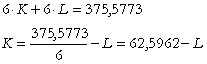
Constatam urmatoarele:
fata de echilibrul initial, prin efectul de substituire
s-a schimbat panta curbei isocost, costul total scazand;
s-a
schimbat echilibrul de la ![]()
![]() la
la ![]() ,
, ![]() ;
;
volumul productiei a ramas constant.
fata de echilibrul initial, prin variatia reziduala, prin efectul de substituire si variatia de compensare a cheltuielilor:
costul total a ramas constant
a
scazut ![]() de la 26,82 la 26,81
de la 26,82 la 26,81
a
crescut ![]() de la 26,82 la 36,42
de la 26,82 la 36,42
volumul productiei a crescut de la 100 u.f. la 127,99 u.f.
|
Politica de confidentialitate
|
Despre managementul investitiilor |
||||||||||
Stiu si altele ... |
||||||||||
|
||||||||||